题目内容
7.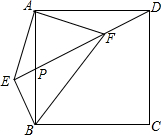 如图,正方形ABCD中,P为AB中点,BE⊥DP交DP延长线于E,连结AE,AF⊥AE交DP于F,连结BF,CF.下列结论:①EF=$\sqrt{2}$AF;②AB=FB;③CF∥BE;④EF=CF.其中正确的结论有( )个.
如图,正方形ABCD中,P为AB中点,BE⊥DP交DP延长线于E,连结AE,AF⊥AE交DP于F,连结BF,CF.下列结论:①EF=$\sqrt{2}$AF;②AB=FB;③CF∥BE;④EF=CF.其中正确的结论有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据已知和正方形的性质推出∠EAB=∠DAF,∠EBA=∠ADP,AB=AD,证△ABE≌△ADF即可;取EF的中点M,连接AM,推出AM=MF=EM=DF,证∠AMB=∠FMB,BM=BM,AM=MF,推出△ABM≌△FBM即可;求出∠FDC=∠EBF,推出△BEF≌△DFC即可.
解答 解:在正方形ABCD中,AB=AD,∠BAD=90°,
∴∠DAF+∠BAF=90°,
∵AF⊥AE,
∴∠BAE+∠BAF=90°,
∴∠BAE=∠DAF,
∵BE⊥DP,
∴∠ABE+∠BPE=90°,
又∵∠ADF+∠APD=90°,∠BPE=∠APD,
∴∠ABE=∠ADF,
在△ABE和△ADF中,
$\left\{\begin{array}{l}{∠ABE=∠ADF}\\{AB=AD}\\{∠BAE=∠DAF}\end{array}\right.$,
∴△ABE≌△ADF(ASA),
∴AE=AF,
∴△AEF是等腰直角三角形,
∴EF=$\sqrt{2}$AF;故①正确;
∴AE=AF,BE=DF,
∴∠AEF=∠AFE=45°,
取EF的中点M,连接AM,
∴AM⊥EF,AM=EM=FM,
∴BE∥AM,
∵AP=BP,
∴AM=BE=DF,
∴∠EMB=∠EBM=45°,
∴∠AMB=90°+45°=135°=∠FMB,
在△ABM和△FBM中,
$\left\{\begin{array}{l}{AM=FM}\\{∠AMB=∠FMB}\\{BM=BM}\end{array}\right.$,
∴△ABM≌△FBM(SAS),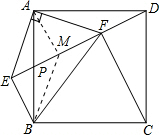
∴AB=BF,故②正确;
∴∠BAM=∠BFM,
∵∠BEF=90°,AM⊥EF,
∴∠BAM+∠APM=90°,∠EBF+∠EFB=90°,
∴∠APF=∠EBF,
∵AB∥CD,
∴∠APD=∠FDC,
∴∠EBF=∠FDC,
在△BEF和△DFC中,
$\left\{\begin{array}{l}{BE=DF}\\{∠EBF=∠FDC}\\{BF=DC}\end{array}\right.$,
∴△BEF≌△DFC(SAS),
∴CF=EF,∠DFC=∠FEB=90°,
故④正确;
∴CF⊥DE,
∵BE⊥DP,
∴CF∥BE;故③正确.
故选D.
点评 此题属于四边形的综合题.考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的性质以及直角三角形的性质等知识.注意准确作出辅助线是解此题的关键.

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案| A. | 6x2-8x=x(6x-8) | B. | a2+4b2-4ab=(a-2b)2 | ||
| C. | 8xyz-6x2y2=2xyz(4-3xy) | D. | 4a2-b2=(4a-b)(4a+b) |
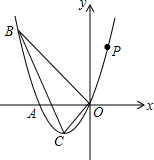 如图,已知抛物线经过点A(-2,0),点B(-3,3)及原点O,顶点为C.
如图,已知抛物线经过点A(-2,0),点B(-3,3)及原点O,顶点为C.