题目内容
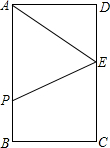 如图,矩形ABCD中,AB=12cm,BC=8cm,E为CD的中点.点P从A点出发,沿A-B-C的方向在矩形边上匀速运动,速度为1cm/s,运动到C点停止.设点P运动的时间为ts.
如图,矩形ABCD中,AB=12cm,BC=8cm,E为CD的中点.点P从A点出发,沿A-B-C的方向在矩形边上匀速运动,速度为1cm/s,运动到C点停止.设点P运动的时间为ts.(1)当P在AB上,t为何值时,△APE的面积是矩形ABCD面积的
| 1 |
| 3 |
(2)整个运动过程中,t为何值时,△APE为等腰三角形?
考点:矩形的性质
专题:动点型
分析:(1)求出矩形的面积,即可得出关于t的方程,求出方程的解即可;
(2)当P在AB上时,分为AP=AE,AP=PE,AE=PE三种情况,画出图形,根据等腰三角形的性质得出即可;当P在BC上时,根据AP、AE、PE的长度大小得出即可.
(2)当P在AB上时,分为AP=AE,AP=PE,AE=PE三种情况,画出图形,根据等腰三角形的性质得出即可;当P在BC上时,根据AP、AE、PE的长度大小得出即可.
解答:解:(1)∵矩形ABCD中,AB=12cm,BC=8cm,
∴矩形ABCD的面积S=12cm×8cm=96cm2,
则
t×1×8=
×96,
解得:t=8,
即当P在AB上,t为8时,△APE的面积是矩形ABCD面积的
;
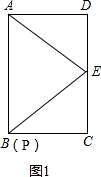
(2)如图1:
∵四边形ABCD是矩形,
∴AD=BC=8cm,CD=AB=12cm,∠C=∠D=∠ABC=90°,
∵E为CD的中点,
∴DE=CE=6cm,
由勾股定理得:AE=BE=10cm,
分为两种情况:第一种情况:当P在AB上时,①如图1,当P和B重合时,AE=PE,此时△APE是等腰三角形,
此时t=12;
②如图2:
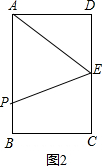
当AP=AE=10cm,此时△APE是等腰三角形,
此时t=10;
③如图3:
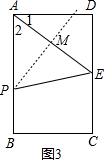
作AE的垂直平分线,交AE于M,交AB于P,此时AP=PE,△APE是等腰三角形,
则∠PAD=∠D=∠PMA=90°,AM=ME=
AE=5cm,
∵∠1+∠2=90°,∠2+∠APM=90°,
∴∠1=∠APM,
∴△APM∽△EAD,
∴
=
,
∴
=
,
∴AP=12.5,
即t=12.5;
第二种情况:当P当P在BC上时,如图4:
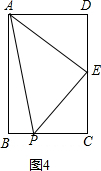
∵AE=10cm,AP>AB,PE<PB,
∴AP>12cm,PE<10cm,
即此时AE、AP、PE不相等,
即P在BC上时,△APE不能为等腰三角形;
综合上述:整个运动过程中,t为12或10或12.5时,△APE为等腰三角形.
∴矩形ABCD的面积S=12cm×8cm=96cm2,
则
| 1 |
| 2 |
| 1 |
| 3 |
解得:t=8,
即当P在AB上,t为8时,△APE的面积是矩形ABCD面积的
| 1 |
| 3 |
(2)如图1:

∵四边形ABCD是矩形,
∴AD=BC=8cm,CD=AB=12cm,∠C=∠D=∠ABC=90°,
∵E为CD的中点,
∴DE=CE=6cm,
由勾股定理得:AE=BE=10cm,
分为两种情况:第一种情况:当P在AB上时,①如图1,当P和B重合时,AE=PE,此时△APE是等腰三角形,
此时t=12;
②如图2:

当AP=AE=10cm,此时△APE是等腰三角形,
此时t=10;
③如图3:

作AE的垂直平分线,交AE于M,交AB于P,此时AP=PE,△APE是等腰三角形,
则∠PAD=∠D=∠PMA=90°,AM=ME=
| 1 |
| 2 |
∵∠1+∠2=90°,∠2+∠APM=90°,
∴∠1=∠APM,
∴△APM∽△EAD,
∴
| AP |
| AE |
| AM |
| DE |
∴
| AP |
| 10 |
| 5 |
| 4 |
∴AP=12.5,
即t=12.5;
第二种情况:当P当P在BC上时,如图4:

∵AE=10cm,AP>AB,PE<PB,
∴AP>12cm,PE<10cm,
即此时AE、AP、PE不相等,
即P在BC上时,△APE不能为等腰三角形;
综合上述:整个运动过程中,t为12或10或12.5时,△APE为等腰三角形.
点评:本题考查了矩形的性质,等腰三角形的性质的应用,能求出符合条件的所有情况是解此题的关键,用了分类讨论思想,有一定的难度.

练习册系列答案
相关题目
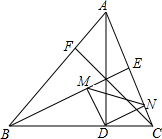 如图,锐角△ABC中,AD,BE,CF是三条高,DM⊥BE于M,DN⊥CF于N
如图,锐角△ABC中,AD,BE,CF是三条高,DM⊥BE于M,DN⊥CF于N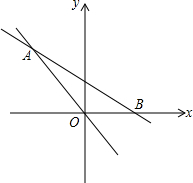 已知,正比例函数y=k1x和一次函数y=k2x+br的图象如图所示,它们的交点A(-3,4),且OB=
已知,正比例函数y=k1x和一次函数y=k2x+br的图象如图所示,它们的交点A(-3,4),且OB=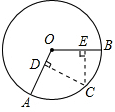 如图,点C是
如图,点C是
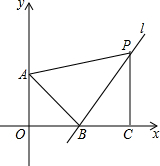 如图,在平面直角坐标系中,O是坐标原点,点A,B的坐标分别是(0,3)(4,0),作直线l垂直AB,点P是直线l上的一个动点,作PC垂直x轴,垂足为C,连接AP,设点P的横坐标为a,在x轴上取点Q,使得以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标.
如图,在平面直角坐标系中,O是坐标原点,点A,B的坐标分别是(0,3)(4,0),作直线l垂直AB,点P是直线l上的一个动点,作PC垂直x轴,垂足为C,连接AP,设点P的横坐标为a,在x轴上取点Q,使得以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标.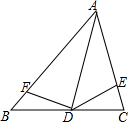 如图,CE=BF,且S△DCE=S△DBF,求证:AD平分∠BAC.
如图,CE=BF,且S△DCE=S△DBF,求证:AD平分∠BAC.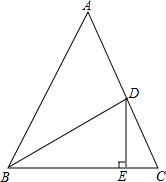 已知△ABC中,BD平分∠ABC,DE⊥BC于E点,且DE:BD=1:2,DC:AD=3:4,CE=
已知△ABC中,BD平分∠ABC,DE⊥BC于E点,且DE:BD=1:2,DC:AD=3:4,CE=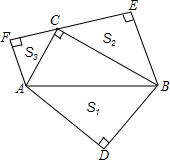 如图,在Rt△ABC中,∠ACB=90°,分别以AB、BC、AC为斜边向外作等腰直角三角形,设所作的△ABD、△BCE、△ACF的面积分别为S1、S2、S3,求证:S1=S2+S3.
如图,在Rt△ABC中,∠ACB=90°,分别以AB、BC、AC为斜边向外作等腰直角三角形,设所作的△ABD、△BCE、△ACF的面积分别为S1、S2、S3,求证:S1=S2+S3.