题目内容
2．某市出租车的收费标准是：起步价8元（即行驶距离不超过3千米都需付8元车费），超过3千米以后，每增加1千米，加收1.5元（不足1千米按1千米计）．某人从甲地到乙地经过的路程是x千米，出租车费为15.5元，那么x的最大值是（ ）| A． | 5 | B． | 7 | C． | 8 | D． | 11 |
分析 已知从甲地到乙地共需支付车费15.5元，从甲地到乙地经过的路程为x千米，首先去掉前3千米的费用，从而根据题意列出不等式，从而得出答案．
解答 解：设某人从甲地到乙地经过的路程是x千米，根据题意，
得：8+1.5（x-3）≤15.5，
解得：x≤8，
即x的最大值为8km，
故选：C．
点评 此题主要考查了一元一次不等式的应用，根据题意明确其收费标准分两部分是完成本题的关键．
练习册系列答案
相关题目
13．
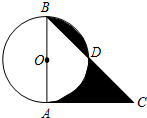如图，在⊙O中，直径AB=2，CA切⊙O于A，BC交⊙O于D，若∠C=45°，则图中阴影部分的面积为（ ）
如图，在⊙O中，直径AB=2，CA切⊙O于A，BC交⊙O于D，若∠C=45°，则图中阴影部分的面积为（ ）| A． | $\frac{π}{2}$ | B． | 2 | C． | π | D． | 1 |
17．在直角坐标系中，点P（2x-3，x-4）在第四象限，则x的取值范围是（ ）
| A． | $\frac{3}{2}$＜x＜4 | B． | $\frac{3}{2}$≤x＜4 | C． | $\frac{3}{2}$＜x≤4 | D． | $\frac{3}{2}$≤x≤4 |
14．8的立方根是（ ）
| A． | ±2 | B． | 2 | C． | -2 | D． | $\sqrt{2}$ |
11．已知关于x的方程3x+m=x+3的解为非负数，且m为正整数，则m的取值为（ ）
| A． | 1 | B． | 1、2 | C． | 1、2、3 | D． | 0、1、2、3 |
12．甲、乙两个城市，乙城市位于甲城市北偏东30°方向，距离为80km，那么甲城市位于乙城市（ ）
| A． | 南偏东30°方向，距离为80km | B． | 南偏西30°方向，距离为80km | ||
| C． | 南偏东60°方向，距离为80km | D． | 南偏西60°方向，距离为80km |