题目内容
12．
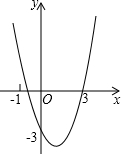如图，抛物线过（-1，0），（3，0），（0，-3）三点，沿x轴方向平移抛物线，使得以平移后的抛物线与x轴、y轴的三个交点为顶点的三角形面积为4，则符合条件的平移方式有（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 由抛物线与x轴的两交点之间的距离恒为4，结合平移后的抛物线与x轴、y轴的三个交点为顶点的三角形面积为4，即可得出平移后的抛物线过点（0，-2），依此画出图形，利用数形结合即可得出结论．
解答 解：∵抛物线与x轴的两交点之间的距离恒为3-（-1）=4，
∴当抛物线与y轴的交点为（0，-2）时，平移后的抛物线与x轴、y轴的三个交点为顶点的三角形面积为4，
∴有两种平移方式，可使平移后的抛物线过点（0，-2）．
故选B．
点评 本题考查了抛物线与x轴的交点以及二次函数图象与几何变换，根据三角形的面积为4，找出平移后的抛物线过点（0，-2）是解题的关键．
练习册系列答案
相关题目
5．在平面直角坐标系中．对于平面内任一点（m，n），规定以下两种变换：
①f（m，n）=（m，-n），如f（2，1）=（2，-1）；
②g（m，n）=（-m，-n），如g（2，1）=（-2，-1）．
按照以上变换有：f[g（3，4）]=f（-3，-4）=（-3，4），那么g[f（3，2）]等于（ ）
①f（m，n）=（m，-n），如f（2，1）=（2，-1）；
②g（m，n）=（-m，-n），如g（2，1）=（-2，-1）．
按照以上变换有：f[g（3，4）]=f（-3，-4）=（-3，4），那么g[f（3，2）]等于（ ）
| A． | （3，2） | B． | （3．-2） | C． | （-3，2） | D． | （-3，-2） |
17．计算：|-2+1|=（ ）
| A． | -1 | B． | 1 | C． | -3 | D． | 3 |
2．已知n是一个正整数，$\sqrt{12n}$是整数，则n的最小值是（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
19．
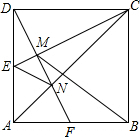如图，在正方形ABCD中，E为AD的中点，DF⊥CE于M，交AC于点N，交AB于点F，连接EN、BM．有如下结论：①△ADF≌△DCE；②MN=FN；③△DMC∽△EMN；④BM=AB；其中正确结论的个数为（ ）
如图，在正方形ABCD中，E为AD的中点，DF⊥CE于M，交AC于点N，交AB于点F，连接EN、BM．有如下结论：①△ADF≌△DCE；②MN=FN；③△DMC∽△EMN；④BM=AB；其中正确结论的个数为（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
19．买书包和文具盒共50个，其中文具盒的数量是书包的3倍多2个，求书包和文具盒各买多少个？若设买书包x个，买文具盒y个，则列出的方程组应是（ ）
| A． | $\left\{\begin{array}{l}{x+y=50}\\{x=3y-2}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=50}\\{x=3y+2}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x+y=50}\\{y=3x-2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=50}\\{y=3x+2}\end{array}\right.$ |