题目内容
 将连续奇数按下面方式排列:用一个如图所示的平行四边行框出九个数,能否使框出的九个自然数之和等于(1)1998;(2)2295;(3)2601?若能,请求出最小的数;若不能,请说明理由.
将连续奇数按下面方式排列:用一个如图所示的平行四边行框出九个数,能否使框出的九个自然数之和等于(1)1998;(2)2295;(3)2601?若能,请求出最小的数;若不能,请说明理由.考点:一元一次方程的应用
专题:
分析:找到9个数与中间的数的关系,用代数式表示出9个数的和,然后代入数据若能求得n的值为奇数,则可以,否则不可以.
解答:解:设中间数为n,则这九个数依次是
(n-18),(n-16),(n-14),(n-2),n,(n+2),(n+14),(n+16),(n+18).
则这9个数之和为9n.
当9n=1998时,n=222,为偶数,故9个数的和不可以是1998;
当9n=2295时,n=255,为奇数,故9个数的和可以2295,最小的数为n-18=255-18=237;
当9n=2601时,n=289,为奇数,故9个数的和可以2601,最小的数为n-18=289-18=271;
(n-18),(n-16),(n-14),(n-2),n,(n+2),(n+14),(n+16),(n+18).
则这9个数之和为9n.
当9n=1998时,n=222,为偶数,故9个数的和不可以是1998;
当9n=2295时,n=255,为奇数,故9个数的和可以2295,最小的数为n-18=255-18=237;
当9n=2601时,n=289,为奇数,故9个数的和可以2601,最小的数为n-18=289-18=271;
点评:此题主要考查学生对数字的变化类知识及一元一次方程的应用,此题的突破点是;设中间数为n,则这九个数依次是(n-18),(n-16),(n-14),(n-2),n,(n+2),(n+14),(n+16),(n+18).此题步骤繁琐,难度较大,是一道难题.

练习册系列答案
相关题目
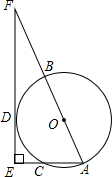 如图,AB是⊙O的直径,AC为弦,D是
如图,AB是⊙O的直径,AC为弦,D是
 如图,在△ABC中,D、E、F分别是AB、BC、AC的中点,AB=6,AC=8,DF=5,求AE的长.
如图,在△ABC中,D、E、F分别是AB、BC、AC的中点,AB=6,AC=8,DF=5,求AE的长.