题目内容
如图甲,在平面直角坐标系中,直线y=-x+8分别交x轴、y轴于点A、B,⊙O的半径为2
个单位长度.点P为直线y=-x+8上的动点,过点P作⊙O的切线PC、PD,切点分别为C、D,且PC⊥PD.
(1)试说明四边形OCPD的形状(要有证明过程);
(2)求点P的坐标;
(3)如图乙,若直线y=-x+b将⊙O的圆周分成两段弧长之比为1:3,请直接写出b的值;
(4)向右移动⊙O(圆心O始终保持在x轴上),试求出当⊙O与直线y=-x+8有交点时圆心O的横坐标m的取值范围.

| 5 |
(1)试说明四边形OCPD的形状(要有证明过程);
(2)求点P的坐标;
(3)如图乙,若直线y=-x+b将⊙O的圆周分成两段弧长之比为1:3,请直接写出b的值;
(4)向右移动⊙O(圆心O始终保持在x轴上),试求出当⊙O与直线y=-x+8有交点时圆心O的横坐标m的取值范围.

考点:圆的综合题
专题:
分析:(1)利用切线的性质和切线长定理可判定出四边形OCPD为正方形;
(2)设P点坐标为(x,-x+8),在Rt△OCP中利用勾股定理得到关于x的方程,求解即可;
(3)设直线y=-x+b与圆交与点E,F,由条件可知∠EOF为90°,可求出OE=OF,进一步可求得b的值;
(4)设向右移动⊙O到O′时,⊙O与直线y=-x+8相切,切点为D,根据相切时圆心O的横坐标即可求得⊙O与直线y=-x+8相交时圆心O的横坐标m的取值范围.
(2)设P点坐标为(x,-x+8),在Rt△OCP中利用勾股定理得到关于x的方程,求解即可;
(3)设直线y=-x+b与圆交与点E,F,由条件可知∠EOF为90°,可求出OE=OF,进一步可求得b的值;
(4)设向右移动⊙O到O′时,⊙O与直线y=-x+8相切,切点为D,根据相切时圆心O的横坐标即可求得⊙O与直线y=-x+8相交时圆心O的横坐标m的取值范围.
解答:解:(1)四边形OCPD是正方形.证明过程如下:
如图甲,连接OC、OD,
∵PC、PD是⊙O的两条切线,
∴∠PCO=∠PDO=90°.
又∵PC⊥PD,
∴四边形OCPD是矩形,
又∵OC=OD,
∴四边形OCPD是正方形;
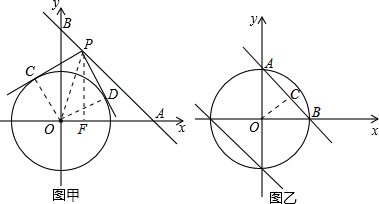
(2)如图甲,过P作x轴的垂线,垂足为F,连接OP.
∵PC、PD是⊙O的两条切线,∠CPD=90°,
∴∠OPD=∠OPC=
∠CPD=45°,
∵∠PDO=90°,∠POD=∠OPD=45°,
∴OD=PD=2
,OP=2
,
∵P在直线y=-x+8上,设P(m,-m+8),则OF=m,PF=-m+8,
∵∠PFO=90°,OF2+PF2=PO2,
∴m2+(-m+8)2=(2
)2,
解得m=2或6,
∴P的坐标为(2,6)或(6,2);
(3)设直线y=-x+b与圆交与点E,F,
若直线y=-x+b将⊙O的圆周分成两段弧长之比为1:3,
则∠EOF=90°,
∴OE=OF=|b|,
∴|b|=2
,
解得b=±2
;
(4)设向右移动⊙O到O′时,⊙O′与直线y=-x+8相切,切点为D,如图3,
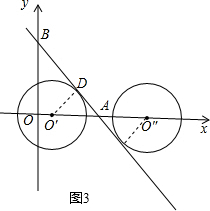
∴O′D⊥AB,
由直线y=-x+8可知A(8,0),B(0,-8),
∴OA=OB,
∴△AOB是等腰直角三角形,
∴∠OAB=45°,
∴△O′AD是等腰直角三角形,
∴O′D=AD=2
,
∴O′A=2
,
∴OO′=8-2
或8+2
,
∴当⊙O与直线y=-x+8相交时圆心O的横坐标m的取值范围为:8-2
≤m≤8+2
.
如图甲,连接OC、OD,
∵PC、PD是⊙O的两条切线,
∴∠PCO=∠PDO=90°.
又∵PC⊥PD,
∴四边形OCPD是矩形,
又∵OC=OD,
∴四边形OCPD是正方形;

(2)如图甲,过P作x轴的垂线,垂足为F,连接OP.
∵PC、PD是⊙O的两条切线,∠CPD=90°,
∴∠OPD=∠OPC=
| 1 |
| 2 |
∵∠PDO=90°,∠POD=∠OPD=45°,
∴OD=PD=2
| 5 |
| 10 |
∵P在直线y=-x+8上,设P(m,-m+8),则OF=m,PF=-m+8,
∵∠PFO=90°,OF2+PF2=PO2,
∴m2+(-m+8)2=(2
| 10 |
解得m=2或6,
∴P的坐标为(2,6)或(6,2);
(3)设直线y=-x+b与圆交与点E,F,
若直线y=-x+b将⊙O的圆周分成两段弧长之比为1:3,
则∠EOF=90°,
∴OE=OF=|b|,
∴|b|=2
| 5 |
解得b=±2
| 5 |
(4)设向右移动⊙O到O′时,⊙O′与直线y=-x+8相切,切点为D,如图3,

∴O′D⊥AB,
由直线y=-x+8可知A(8,0),B(0,-8),
∴OA=OB,
∴△AOB是等腰直角三角形,
∴∠OAB=45°,
∴△O′AD是等腰直角三角形,
∴O′D=AD=2
| 5 |
∴O′A=2
| 10 |
∴OO′=8-2
| 10 |
| 10 |
∴当⊙O与直线y=-x+8相交时圆心O的横坐标m的取值范围为:8-2
| 10 |
| 10 |
点评:本题主要考查圆的切线的性质及直线和圆的位置关系、正方形的判定和性质等知识的综合应用,掌握切线的性质及特殊四边形的判定方法是解题的关键,注意相切时,有圆在直线的左侧和右侧两种情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
“a与5的差的
”可表示为( )
| 1 |
| 2 |
A、a-
| ||
| B、2a-5 | ||
C、
| ||
D、
|
 将连续奇数按下面方式排列:用一个如图所示的平行四边行框出九个数,能否使框出的九个自然数之和等于(1)1998;(2)2295;(3)2601?若能,请求出最小的数;若不能,请说明理由.
将连续奇数按下面方式排列:用一个如图所示的平行四边行框出九个数,能否使框出的九个自然数之和等于(1)1998;(2)2295;(3)2601?若能,请求出最小的数;若不能,请说明理由. 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足 如图,AB是半圆O的直径,矩形EJOM、KOGF、HOQD的顶点E、F、D均在圆上,比较JM、KG、HQ的大小关系并说明理由.
如图,AB是半圆O的直径,矩形EJOM、KOGF、HOQD的顶点E、F、D均在圆上,比较JM、KG、HQ的大小关系并说明理由.