题目内容
 如图,在△ABC中,D、E、F分别是AB、BC、AC的中点,AB=6,AC=8,DF=5,求AE的长.
如图,在△ABC中,D、E、F分别是AB、BC、AC的中点,AB=6,AC=8,DF=5,求AE的长.考点:三角形中位线定理,勾股定理的逆定理
专题:
分析:由条件可得BC=2DF=10,由勾股定理的逆定理可知△ABC为直角三角形,且AE为斜边上的中线,可知AE=
BC=5.
| 1 |
| 2 |
解答:解:
∵D、F为AB、AC的中点,
∴DF为△ABC的中位线,
∴BC=2DF=10,且AB=6,AC=8,
∴AB2+AC2=BC2,
∴△ABC为直角三角形,
∵E为BC中点,
∴AE=
BC=5.
∵D、F为AB、AC的中点,
∴DF为△ABC的中位线,
∴BC=2DF=10,且AB=6,AC=8,
∴AB2+AC2=BC2,
∴△ABC为直角三角形,
∵E为BC中点,
∴AE=
| 1 |
| 2 |
点评:本题主要考查三角形中位线定理及直角三角形的判定,由条件求出BC的长判定出△ABC为直角三角形是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
下列事件中,是必然事件的是( )
| A、打开电视机,正在播放新闻 |
| B、在同一年出生的367名学生中,至少有两人的生日是同一天 |
| C、通过长期努力学习,你会成为数学家 |
| D、下雨天,每个人都打着雨伞 |
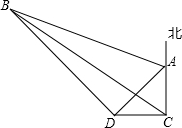 一船在海面C处看见一灯塔A在它的正北方向,另一个灯塔B在它的北偏西60°,此船在正西航行1海里后到D,这时灯塔A、B分别在它的东北、西北方向,求这两个灯塔间的距离(结果保留根号).
一船在海面C处看见一灯塔A在它的正北方向,另一个灯塔B在它的北偏西60°,此船在正西航行1海里后到D,这时灯塔A、B分别在它的东北、西北方向,求这两个灯塔间的距离(结果保留根号). 如图,在△ABC中,若∠B=2∠C,AD⊥BC,E为BC边中点,求证:AB=2DE.
如图,在△ABC中,若∠B=2∠C,AD⊥BC,E为BC边中点,求证:AB=2DE. 将连续奇数按下面方式排列:用一个如图所示的平行四边行框出九个数,能否使框出的九个自然数之和等于(1)1998;(2)2295;(3)2601?若能,请求出最小的数;若不能,请说明理由.
将连续奇数按下面方式排列:用一个如图所示的平行四边行框出九个数,能否使框出的九个自然数之和等于(1)1998;(2)2295;(3)2601?若能,请求出最小的数;若不能,请说明理由.