题目内容
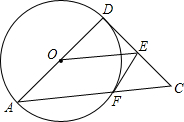 如图,已知Rt△ADC中,∠D=90°,以AD为直径的⊙O交斜边AC于F,OE∥AC,交DC于E.
如图,已知Rt△ADC中,∠D=90°,以AD为直径的⊙O交斜边AC于F,OE∥AC,交DC于E.(1)求证:EF为⊙O的切线;
(2)求证:2EF2=CF•OE.
考点:切线的判定,相似三角形的判定与性质
专题:证明题
分析:(1)连接OF、DF交OE于点G,在△ODF和△EFD中,利用等边对等角证明∠ODF=∠OFD,∠EDF=∠EFD,则∠OFE=∠ODC=90°,从而证得;
(2)利用切割线定理,以及直角三角形斜边上的中线等于斜边的一半,利用CD分别表示出2EF2和CF•OE,即可证得.
(2)利用切割线定理,以及直角三角形斜边上的中线等于斜边的一半,利用CD分别表示出2EF2和CF•OE,即可证得.
解答: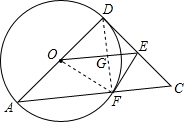 证明:(1)连接OF、DF交OE于点G.
证明:(1)连接OF、DF交OE于点G.
∵AD是圆的直径,
∴∠AFD=90°,即∠DF⊥AC,
又∵OE∥AC,
∴OE⊥DF,
又∵OD=OF,
∴DG=GF,∠ODF=∠OFD,
∴DE=EF,
∴∠EDF=∠EFD,
∴∠OFE=∠ODC=90°,
∴OF⊥EF,则EF是圆的切线;
(2)证明:∵O是AB的中点,OE∥AC,
∴OE是△ABC的中位线,
∴OE=
AC,即AC=2OE,
又∵CD是圆的切线,
∴CD2=CF•AC=2CF•OE,即CF•OE=
CD2.
∵在直角△DFC中,E是CD的中点,
∴EF=
CD,即CD=2EF,
∴2EF2=
CD2,
∴2EF2=CF•OE.
 证明:(1)连接OF、DF交OE于点G.
证明:(1)连接OF、DF交OE于点G.∵AD是圆的直径,
∴∠AFD=90°,即∠DF⊥AC,
又∵OE∥AC,
∴OE⊥DF,
又∵OD=OF,
∴DG=GF,∠ODF=∠OFD,
∴DE=EF,
∴∠EDF=∠EFD,
∴∠OFE=∠ODC=90°,
∴OF⊥EF,则EF是圆的切线;
(2)证明:∵O是AB的中点,OE∥AC,

∴OE是△ABC的中位线,
∴OE=
| 1 |
| 2 |
又∵CD是圆的切线,
∴CD2=CF•AC=2CF•OE,即CF•OE=
| 1 |
| 2 |
∵在直角△DFC中,E是CD的中点,
∴EF=
| 1 |
| 2 |
∴2EF2=
| 1 |
| 2 |
∴2EF2=CF•OE.
点评:本题考查了切线的判定定理、切割线定理和直角三角形的性质定理,利用CD分别表示出2EF2和CF•OE是关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
估算
的值在( )
| 24 |
| A、在4和5之间 |
| B、在5和6之间 |
| C、在6和7之间 |
| D、在3和4之间 |
 如图,已知?ABCD中,AB=8cm,AD=6cm,CE平分∠BCD交AB于点E,则线段AE的长为( )
如图,已知?ABCD中,AB=8cm,AD=6cm,CE平分∠BCD交AB于点E,则线段AE的长为( )| A、1cm | B、2cm |
| C、3cm | D、4cm |
 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:DB=3:1,AC=12,求EC的长度.
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:DB=3:1,AC=12,求EC的长度. 如图,双曲线y=
如图,双曲线y=