题目内容
如图，已知?ABCD中，AB=8cm，AD=6cm，CE平分∠BCD交AB于点E，则线段AE的长为（ ）| A、1cm | B、2cm |
| C、3cm | D、4cm |
考点：平行四边形的性质
专题：
分析：利用角平分线的性质以及平行线的性质得出∠BCE=∠BEC，进而得出BC=BE，再利用平行四边形的性质求出即可．
解答：解：∵CE平分∠BCD交AB于点E，
∴∠DCE=∠BCE，
∵DC∥AB，
∴∠DCE=∠CEB，
∴∠BCE=∠BEC，
∴BC=BE，
∵四边形ABCD是平行四边形，
∴AD=BC，AB=DC，
∴BC=BE=6cm，
∴AE=AB-BE=8-6=2（cm）．
故选：B．
∴∠DCE=∠BCE，
∵DC∥AB，
∴∠DCE=∠CEB，
∴∠BCE=∠BEC，
∴BC=BE，
∵四边形ABCD是平行四边形，
∴AD=BC，AB=DC，
∴BC=BE=6cm，
∴AE=AB-BE=8-6=2（cm）．
故选：B．
点评：此题主要考查了平行四边形的性质以及平行线和角平分线的性质，得出BC=BE是解题关键．
练习册系列答案
一本好题口算题卡系列答案
相关题目
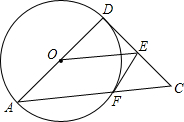如图，已知Rt△ADC中，∠D=90°，以AD为直径的⊙O交斜边AC于F，OE∥AC，交DC于E．
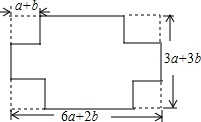如图，李师傅把一块长方形（边长分别为6a+2b和3a+3b）铁皮的四个角各剪去一个边长为（a+b）的小正方形，然后折成一个无盖的盒子．若关于x的一元二次方程x2-x-m=0的一个根是x=1，则m的值是（ ）
| A、1 | B、0 | C、-1 | D、2 |
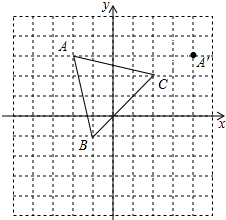在平面直角坐标系中，△ABC的三个顶点的位置如图所示（顶点在格点上）．现将△ABC沿某直线翻折，使点A变换为点A′，A点坐标为（-2，3），A′的坐标为（4，3）．