题目内容
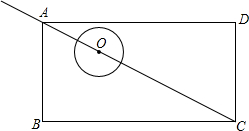 如图,在矩形ABCD中,AB=3,BC=6.点O为圆心,1为半径的圆,沿射线CA平移.若在平移过程中⊙O与矩形的边只有一个公共点的情况出现了a次,则a的值为
如图,在矩形ABCD中,AB=3,BC=6.点O为圆心,1为半径的圆,沿射线CA平移.若在平移过程中⊙O与矩形的边只有一个公共点的情况出现了a次,则a的值为考点:直线与圆的位置关系
专题:计算题
分析:作OE⊥AD于E,OF⊥AB于F,如图,用勾股定理计算出AC=3
,然后利用切线的性质可分别计算出⊙A与各边相切时的AO的值,从而得到a的值.
| 5 |
解答:解:作OE⊥AD于E,OF⊥AB于F, 如图,
如图,
在Rt△ABC中,∵AB=3,BC=6,
∴AC=
=3
,
当OF=1时,⊙O与AD相切,⊙O与矩形的边AD只有一个公共点,
∵OF∥CD,
∴
=
,即
=
,解得AO=
;
当OE=1时,⊙O与AB相切,⊙O与矩形的边AB只有一个公共点,用同样的方法可计算出AO=
,
同理可得当AO=2
时,⊙A与边CB只有一个公共点;当当AO=
时,⊙A与边CD只有一个公共点,
∴a的值为4.
故答案为4.
 如图,
如图,在Rt△ABC中,∵AB=3,BC=6,
∴AC=
| AB2+BC2 |
| 5 |
当OF=1时,⊙O与AD相切,⊙O与矩形的边AD只有一个公共点,
∵OF∥CD,
∴
| AO |
| AC |
| OF |
| CD |
| AO | ||
3
|
| 1 |
| 3 |
| 5 |
当OE=1时,⊙O与AB相切,⊙O与矩形的边AB只有一个公共点,用同样的方法可计算出AO=
| ||
| 2 |
同理可得当AO=2
| 5 |
5
| ||
| 2 |
∴a的值为4.
故答案为4.
点评:本题考查了直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,当直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.

练习册系列答案
相关题目
已知2x6y2和-
x3myn是同类项,则m、n的值分别是( )
| 1 |
| 3 |
| A、m=-1,n=2 |
| B、m=-2,n=1 |
| C、m=2,n=2 |
| D、m=2,n=1 |
 如图,已知E为?ABCD的边BC延长线上一点,AE交BD于G,交CD于F,求证:AG2=EG•FG.
如图,已知E为?ABCD的边BC延长线上一点,AE交BD于G,交CD于F,求证:AG2=EG•FG.