题目内容
如图，已知E为?ABCD的边BC延长线上一点，AE交BD于G，交CD于F，求证：AG2=EG•FG．考点：相似三角形的判定与性质,平行四边形的性质
专题：证明题
分析：运用平行四边形的性质证明△ADG∽△EBG，△DGF∽△BGA，列出比例式进行比较、分析、归纳、总结，即可解决问题．
解答：证明：∵四边形ABCD是平行四边形，
∴AD∥BE，AB∥DF；
∴△ADG∽△EBG，△DGF∽△BGA，
∴AG：EG=DG：BG，FG：AG=DG：BG，
∴AG：EG=FG：AG，
∴AG2=EG•FG．
证明：∵四边形ABCD是平行四边形，∴AD∥BE，AB∥DF；
∴△ADG∽△EBG，△DGF∽△BGA，
∴AG：EG=DG：BG，FG：AG=DG：BG，
∴AG：EG=FG：AG，
∴AG2=EG•FG．
点评：该题以平行四边形为载体，以考查平行四边形的性质、相似三角形的判定及其性质等几何知识点的应用为核心构造而成；灵活运用有关知识点来分析、判断、推理或解答是解题的关键．
练习册系列答案
相关题目
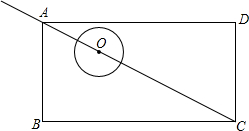如图，在矩形ABCD中，AB=3，BC=6．点O为圆心，1为半径的圆，沿射线CA平移．若在平移过程中⊙O与矩形的边只有一个公共点的情况出现了a次，则a的值为
如图，E为平行四边形ABCD的对角线AC上一点，AE：EC=1：3，BE的延长线交CD的延长线于G，交AD于F，求证：BF：FG=1：2．
如图所示，图中有一个正方形，此正方形的面积是