题目内容
7.已知:某校有31名初二的学生要到教育局参加数学竞赛,该校租用A、B两种型号的车送学生,用2辆A型车和1辆B型车一次只能送10个;用1辆A型车和2辆B型车一次只能送11个,根据以上信息,解答下列问题:(1)1辆A型车和1辆B型车一次可分别送多少个学生?
(2)计划同时租用A型车a辆和B型车b辆,一次送完,且恰好每辆车坐满(不允许超定额载人)请你帮该校设计租车方案;
(3)根据(2)的方案,若A型车每辆需租金每次50元,B型车每辆需租金每次60元,请选出最省钱的租车方案,并求出最少租车费用是多少?
分析 (1)设1辆A型车一次可以送x个学生,1辆B型车一次可以送y个学生,根据“用2辆A型车和1辆B型车一次只能送10个;用1辆A型车和2辆B型车一次只能送11个”即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)由总人数为31即可得出3a+4b=31,进而可得出b=$\frac{31-3a}{4}$,再根据a、b均为正整数即可找出各符合题意的方案;
(3)根据总价=单价×数量分别求出(2)中各方案的总费用,比较后即可得出结论.
解答 解:(1)设1辆A型车一次可以送x个学生,1辆B型车一次可以送y个学生,
根据题意得:$\left\{{\begin{array}{l}{2x+y=10}\\{x+2y=11}\end{array}}\right.$,
解得:$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$.
答:1辆A型车一次可以送3个学生,1辆B型车一次可以送4个学生.
(2)根据题意得:3a+4b=31,
∴b=$\frac{31-3a}{4}$.
∵a、b均为正整数,
∴方案一:当a=1时,b=7;方案二:当a=5时,b=4;方案三:当a=9时,b=1.
(3)由(2)知:
方案一:50×1+60×7=470(元);
方案二:50×5+60×4=490(元);
方案三:50×9+60×1=510(元).
∵470<490<510,
∴选方案一,最少租车费用是470元.
点评 本题考查了二元一次方程组的应用以及二元一次方程的应用,解题的关键是:(1)根据“用2辆A型车和1辆B型车一次只能送10个;用1辆A型车和2辆B型车一次只能送11个”列出关于x、y的二元一次方程组;(2)根据总人数为31找出3a+4b=31;(3)利用总价=单价×数量分别求出(2)中各方案的总费用.

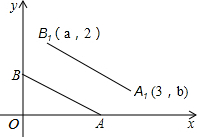 如图,平面直角坐标系中,A、B两点的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,则a,b的值分别为( )
如图,平面直角坐标系中,A、B两点的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,则a,b的值分别为( )| A. | 1,3 | B. | 1,2 | C. | 2,1 | D. | 1,1 |
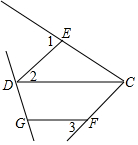 如图,已知∠1=∠ECF,∠2=∠3,那么∠GDC+∠DGF=180°吗?请说明理由.
如图,已知∠1=∠ECF,∠2=∠3,那么∠GDC+∠DGF=180°吗?请说明理由.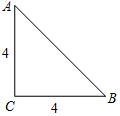 在数学活动课中,同学们准备了一些等腰直角三角形纸片,从每张纸片中剪出一个扇形制作圆锥玩具模型.如图,已知△ABC是腰长为4的等腰直角三角形.
在数学活动课中,同学们准备了一些等腰直角三角形纸片,从每张纸片中剪出一个扇形制作圆锥玩具模型.如图,已知△ABC是腰长为4的等腰直角三角形.