题目内容
3.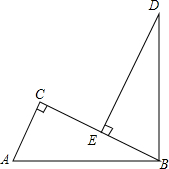 如图,∠ABD=90°,AB=BD,AC⊥BC,DE⊥BC,垂足分别为C、E.求证:AC+CE=DE.
如图,∠ABD=90°,AB=BD,AC⊥BC,DE⊥BC,垂足分别为C、E.求证:AC+CE=DE.
分析 根据垂直的定义得到∠ABC=∠D,进而证得△ABC≌△BDE,根据全等三角形的性质即可证得结论.
解答 证明:∵∠ABD=90°,DE⊥BC,
∴∠ABC=∠D=90°-∠CBD,
在△ABC和△BDE中,
$\left\{\begin{array}{l}{∠C=∠DEB}\\{AB=BD}\\{∠ABC=∠D}\end{array}\right.$,
∴△ABC≌△BDE,
∴AC=BE,BC=DE,
AC+CE=DE.
点评 本题主要考查了互为余角的关系,全等三角形的判定与性质,能根据同角的余角相等证得∠ABC=∠D是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11. 如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,那么此拦水坝斜坡AB的坡度及坡面AB的长分别为( )
如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,那么此拦水坝斜坡AB的坡度及坡面AB的长分别为( )
 如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,那么此拦水坝斜坡AB的坡度及坡面AB的长分别为( )
如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,那么此拦水坝斜坡AB的坡度及坡面AB的长分别为( )| A. | $\frac{\sqrt{3}}{3}$,20m | B. | $\sqrt{3}$,10$\sqrt{3}$m | C. | 30°,20m | D. | 60°,10$\sqrt{3}$m |
12.某同学骑车从学校到家,每分钟行150米,某天回家时,速度提高到每分钟200米,结果提前5分钟到家,设原来从学校到家骑x分钟,则列方程为( )
| A. | 150x=200(x+5) | B. | 150x=200(x-5) | C. | 150(x+5)=200x | D. | 150(x-5)=200x |
 如图中以点A为端点的线段有4条,分别是AB、AE、AD、AC.
如图中以点A为端点的线段有4条,分别是AB、AE、AD、AC.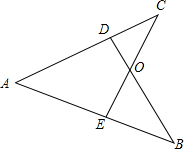 如图,CE⊥AB于E,BD⊥AC于D,BD、CE交于点O,且OD=OE,求证:AB=AC.
如图,CE⊥AB于E,BD⊥AC于D,BD、CE交于点O,且OD=OE,求证:AB=AC.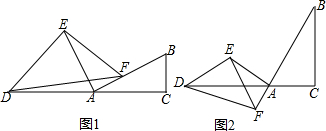
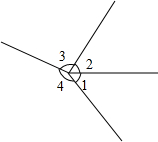 如图,∠1=∠2,且∠2:∠3:∠4=1:2:3,求∠2的度数.
如图,∠1=∠2,且∠2:∠3:∠4=1:2:3,求∠2的度数.