题目内容
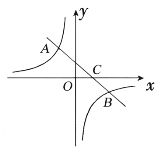
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于二、四象限内的
的图象交于二、四象限内的![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
(1)求该反比例函数和一次函数的解析式;
(2)连接![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
(3)设点![]() 在
在![]() 轴上,且满足
轴上,且满足![]() 是直角三角形,直接写出点
是直角三角形,直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)9;(3)存在,满足条件的
;(2)9;(3)存在,满足条件的![]() 点坐标为
点坐标为![]()
【解析】
(1)先把A(-3,4)代入反比例函数解析式得到m的值,从而确定反比例函数的解析式为y=![]() ;再利用反比例函数解析式确定B点坐标为(6,-2),然后运用待定系数法确定所求的一次函数的解析式为y=
;再利用反比例函数解析式确定B点坐标为(6,-2),然后运用待定系数法确定所求的一次函数的解析式为y=![]() ;
;
(2)先依据一次函数求得点C的坐标,进而得到△AOB 的面积;
(3)过A点作AP1⊥x轴交x轴于P1,AP2⊥AC交x轴于P2,即可得P1点的坐标为(-3,0);再证明Rt△AP2P1∽Rt△CAP1,利用相似比计算出P1P2的长度,进而得到OP2的长度,可得P2点的坐标为![]() ,于是得到满足条件的P点坐标.
,于是得到满足条件的P点坐标.
(1)将![]() 代入
代入![]() ,得
,得![]() .
.
∴反比例函数的解析式为![]() ,
,
将![]() 代入
代入![]() ,
,
得![]()
解得![]()
∴![]()
将![]() 分别代入
分别代入![]() ,得
,得
![]() ,解得
,解得
∴所求的一次函数的解析式为![]()
(2)当![]() 时,
时,![]() ,
,
解得:![]() ,
,
![]()
![]()
∴![]()
(3)存在
∴满足条件的![]() 点坐标为
点坐标为![]() ,理由如下:
,理由如下:
过A点作AP1⊥x轴于P1,AP2⊥AC交x轴于P2,如图,
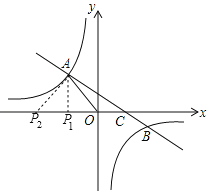
∴∠AP1C=90°,
∵A点坐标为(-3,4),
∴P1点的坐标为(-3,0);
∵∠P2AC=90°,
∴∠P2AP1+∠P1AC=90°,而∠AP2P1+∠P2AP1=90°,
∴∠AP2P1=∠P1AC,
∴Rt△AP2P1∽Rt△CAP1,
∴![]() ,即
,即![]() ,
,
∴P1P2=![]() ,
,
∴OP2=3+![]() =
=![]() ,
,
∴P2点的坐标为(![]() ,0),
,0),
∴满足条件的P点坐标为(-3,0)、(![]() ,0).
,0).

练习册系列答案
相关题目