题目内容
20.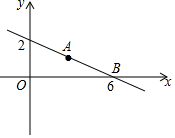 如图,直线y=kx+b经过点A(3,1)和点B(6,0)两点,则不等式0≤kx+b<$\frac{1}{3}$x的解集为1<x≤6.
如图,直线y=kx+b经过点A(3,1)和点B(6,0)两点,则不等式0≤kx+b<$\frac{1}{3}$x的解集为1<x≤6.
分析 根据一次函数图象即可求出该不等式的解集
解答 解:设直线y=$\frac{1}{3}$x,
当x=3时,
y=1,
即直线y=$\frac{1}{3}$x过点A,
∵0≤kx+b<$\frac{1}{3}$x,
即表示函数y=kx+b的图象在x轴上方的部分,且在直线y=$\frac{1}{3}$x下方的部分,
故该不等式的解集为:1<x≤6.
故答案为:1<x≤6
点评 本题考查一次函数与一次不等式的关系,解题的关键是熟练运用一次函数的图象性质,本题属于基础中等题型.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
3.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (-a2)3=-a5 | C. | a10÷a9=a(a≠0) | D. | (-bc)4÷(-bc)2=-b2c2 |
5.已知抛物线y=ax2+bx+c(a<0)过A(-4,1),B(0,1),C(x1,y1),D(x2,y2)四点,且y1<y2,则x1与x2的取值可能是( )
| A. | x1=-1,x2=1 | B. | x1=-5,x2=1 | C. | x1=3,x2=-3 | D. | x1=1,x2=-6 |
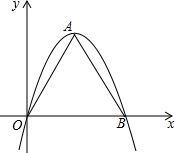 如图一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”
如图一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形” 如图为直线y=ax+b的图象,则不等式ax+b<-1的解集为x>4.
如图为直线y=ax+b的图象,则不等式ax+b<-1的解集为x>4. 如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=4$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.
如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=4$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.