题目内容
6.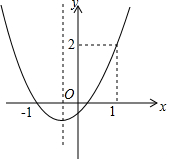 已知抛物线y=ax2+bx+c的图象如图所示,则下列结论:
已知抛物线y=ax2+bx+c的图象如图所示,则下列结论:①abc>0;②a+b+c=2;③b>1;④a<$\frac{1}{2}$.
其中正确的结论是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ②④ |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:①∵抛物线的开口向上,∴a>0,
∵与y轴的交点为在y轴的负半轴上,∴c<0,
∵对称轴为x=$\frac{b}{2a}$<0,∴a、b同号,即b>0,
∴abc<0,
故本选项错误;
②当x=1时,函数值为2,
∴a+b+c=2;
故本选项正确;
③当x=-1时,函数值<0,
即a-b+c<0,(1)
又a+b+c=2,
将a+c=2-b代入(1),
2-2b<0,
∴b>1
故本选项正确;
④∵对称轴x=$-\frac{b}{2a}$>-1,
解得:$\frac{b}{2}$<a,
∵b>1,
∴a>$\frac{1}{2}$,
故本选项错误;
综上所述,其中正确的结论是②③;
故选B.
点评 本题考查的是二次函数图象与系数的关系,关键是记住二次项系数a决定抛物线的开口方向和大小,一次项系数b和二次项系数a共同决定对称轴的位置,常数项c决定抛物线与y轴交点.

练习册系列答案
相关题目
14. 如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )
如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )
 如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )
如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )| A. | (2,-1)或(-2,1) | B. | (8,-4)或(-8,-4) | C. | (2,-1) | D. | (8,-4) |
1.义务教育均衡发展是一种新的教育发展观,是解决我国目前教育问题的新举措.其最终目标,就是要合理配置教育资源,办好每一所学校,教好每一个学生,实现教育公平.我们县级政府为推进义务教育均衡发展工作的评估,今年预算办学经费约为3亿5千万,请你用科学记数法表示应是( )
| A. | 3.5×108 | B. | 3.5×109 | C. | 35×108 | D. | 0.35×109 |
11.在一些汉字的美术字中,有的是轴对称图形.下面五个词中“自由 平等 民主 敬业 友善”可以看作轴对称图形的汉字有( )个.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
18.下列运算正确的是( )
| A. | (a2)3=a5 | B. | a3•a=a4 | C. | (3ab)2=6a2b2 | D. | a6÷a3=a2 |
15.已知反比例函数y=$\frac{k-1}{x}$的图象位于第二、第四象限,那么关于x的一元二次方程x2+2x+k=0的根的情况是( )
| A. | 方程有两个不想等的实数根 | B. | 方程不一定有实数根 | ||
| C. | 方程有两个相等的实数根 | D. | 方程没有实数根 |
 如图,四边形ADBC中,∠D、∠C为直角,G、I分别是△ABC、△ABD的内心,延长AG、BG、AI、BI交四边于Q、E、P、F,如果四边形GAIB的面积为17,求六边形EAFPBQ的面积.
如图,四边形ADBC中,∠D、∠C为直角,G、I分别是△ABC、△ABD的内心,延长AG、BG、AI、BI交四边于Q、E、P、F,如果四边形GAIB的面积为17,求六边形EAFPBQ的面积.


