题目内容
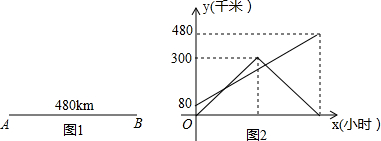
20.如图1,甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,甲车到达C地后因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图2,结合图象信息解答下列问题:(1)乙车的速度是80千米/时,乙车行驶的时间t=6小时;
(2)求甲车从C地按原路原速返回A地的过程中,甲车距它出发地的路程y与它出发的时间x的函数关系式;
(3)直接写出甲车出发多长时间两车相距80千米.
分析 (1)结合题意,利用速度=路程÷时间,可得乙的速度、行驶时间;
(2)找到甲车到达C地和返回A地时x与y的对应值,利用待定系数法可求出函数解析式;
(3)甲、乙两车相距80千米有两种情况:
①相向而行:相等关系为“甲车行驶路程+乙车行驶路程+甲乙间距离=480”,
②同向而行:相等关系为“甲车距它出发地的路程+乙车路程-甲乙间距离=480”
②甲乙相遇之后,甲返回之前:“甲车行驶路程+乙车行驶路程-甲乙间距离=480”
分别根据相等关系列方程可求解.
解答 解:(1)∵乙车比甲车先出发1小时,由图象可知乙行驶了80千米,
∴乙车速度为:80千米/时,乙车行驶全程的时间t=480÷80=6(小时);
(2)根据题意可知甲从出发到返回A地需5小时,
∵甲车到达C地后因立即按原路原速返回A地,
∴结合函数图象可知,当x=$\frac{5}{2}$时,y=300;当x=5时,y=0;
设甲车从C地按原路原速返回A地时,即$\frac{5}{2}$≤x≤5,
甲车距它出发地的路程y与它出发的时间x的函数关系式为:y=kx+b,
将$(\frac{5}{2},300),(5,0)$函数关系式得:$\left\{\begin{array}{l}{\frac{5}{2}k+b=300}\\{5k+b=0}\end{array}$,
解得:$\left\{\begin{array}{l}{k=-120}\\{b=600}\end{array}$,
故甲车从C地按原路原速返回A地时,
甲车距它出发地的路程y与它出发的时间x的函数关系式为:y=-120x+600;
(3)由题意可知甲车的速度为:$\frac{600}{5}$=120(千米/时),
设甲车出发m小时两车相距80千米,有以下两种情况:
①两车相向行驶时,有:120m+80(m+1)+80=480,
解得:m=$\frac{8}{5}$;
②两车同向行驶时,有:600-120m+80(m+1)-80=480,
解得:m=3;
③两车相遇之后,甲返回前,有120m+80(m+1)-80=480,
解得:m=$\frac{12}{5}$;
∴甲车出发$\frac{8}{5}$小时或3小时或$\frac{12}{5}$两车相距80千米.
故答案为:(1)80,6.
点评 本题主要考查了一次函数的应用问题,解答此题的关键是要理解分段函数图象所表示的实际意义,
准确找到等量关系,列方程解决实际问题,属中档题.

 如图,已知⊙O的直径AB经过弦CD的中点E,连接BC、BD,则下列结论错误的是( )
如图,已知⊙O的直径AB经过弦CD的中点E,连接BC、BD,则下列结论错误的是( )| A. | AB⊥CD | B. | BC=BD | C. | ∠BCD=∠BDC | D. | OE=BE |
| A. | a2+a2=a3 | B. | (-a2)2=a4 | C. | ab2•3a2b=3a2b2 | D. | -2a6÷a2=-2a3 |
 如图,直线PA是一次函数y=x+n(n>0)的图象与x轴交于点A(-4,0),直线PB是一次函数y=-2x+m(m>n)的图象与x轴交于点B(3,0).
如图,直线PA是一次函数y=x+n(n>0)的图象与x轴交于点A(-4,0),直线PB是一次函数y=-2x+m(m>n)的图象与x轴交于点B(3,0). 如图所示是由几个小立方体所组成几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的从正面看和从左面看的形状图.
如图所示是由几个小立方体所组成几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的从正面看和从左面看的形状图.
