题目内容
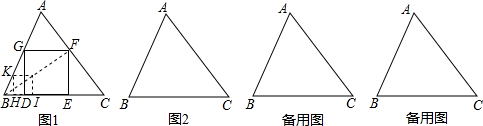
10.已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第2013个图形中直角三角形的个数有( )
| A. | 8048个 | B. | 4024个 | C. | 4026个 | D. | 4028个 |
分析 观察图形可知,两个图形为一个组,直角三角形的个数相同,且都是4的倍数,然后求出第2013个图形的组数,计算即可得解.
解答 解:图①图②的直角三角形的个数相同,都是4,4=4×1,
图③图④的直角三角形的个数相同,都是8,8=4×2,
…,
图2013图2014的直角三角形的个数相同,都是4×$\frac{2014}{2}$=4028个.
故选D.
点评 本题是对图形变化规律的考查,观察图形,得到两个图形的直角三角形的个数相同是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.下列各组的两个数中,运算后结果相等的是( )
| A. | 23和 32 | B. | -33和 (-3)3 | C. | -22和(-2)2 | D. | -|-2|和-(-2) |
5.点M(5,-6)先向右平移3个单位长度再向下平移2个单位长度的点的坐标是( )
| A. | (2,-8) | B. | (8,-8) | C. | (8,-4) | D. | (2,-4) |
15.一个直角三角形的两条直角边相差5cm,面积是7cm2,斜边长是( )
| A. | $\sqrt{14}$ | B. | $\sqrt{35}$ | C. | $\sqrt{53}$ | D. | $\sqrt{74}$ |
20.?ABCD中,AB≠BC,其四个内角的角平分线所围成的四边形一定是( )
| A. | 有一个角为30°的平行四边形 | B. | 有一个角为45°的平行四边形 | ||
| C. | 有一个角为60°的平行四边形 | D. | 矩形 |
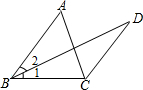 看图填空,并在括号内说明理由:
看图填空,并在括号内说明理由: