题目内容
2.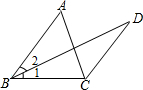 看图填空,并在括号内说明理由:
看图填空,并在括号内说明理由:∵BD平分∠ABC(已知)
∴∠1=∠2(角平分线定义)
又∠1=∠D(已知)
∴∠2=∠D(等量代换)
∴AB∥CD(内错角相等两直线平行)
∴∠ABC+∠BCD=180°(两直线平行同旁内角互补)
又∠ABC=55°(已知)
∴∠BCD=125°.
分析 由BD为角平分线,利用角平分线定义得到一对角相等,再由已知角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到AB与CD平行,利用两直线平行同旁内角互补即可求出所求角的度数.
解答 解:∵BD平分∠ABC(已知)
∴∠1=∠2(角平分线定义)
又∠1=∠D(已知)
∴∠2=∠D(等量代换)
∴AB∥CD(内错角相等两直线平行)
∴∠ABC+∠BCD=180°(两直线平行同旁内角互补)
又∠ABC=55°(已知)
∴∠BCD=125°.
故答案为:∠1;∠2;角平分线定义;∠2;∠D;等量代换;AB;CD;内错角相等两直线平行;∠BCD;两直线平行同旁内角互补;125°.
点评 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
12.如果不等式组$\left\{{\begin{array}{l}{x<3}\\{x>m}\end{array}}\right.$无解,那么m的取值范围是( )
| A. | m≤3 | B. | m≥3 | C. | m>3 | D. | m<3 |
10.已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第2013个图形中直角三角形的个数有( )


| A. | 8048个 | B. | 4024个 | C. | 4026个 | D. | 4028个 |
7.下列从左到右的变形,是分解因式的是( )
| A. | (a+3)(a-3)=a2-9 | B. | x2+x-5=(x-2)(x+3)+1 | C. | a2b+ab2=ab(a+b) | D. | x2+1=x(x+$\frac{1}{x}$) |
14.若(m2+n2)(m2+n2-2)=8,则m2+n2的值为( )
| A. | 4 | B. | 2 | C. | 4或-2 | D. | 2或-4 |
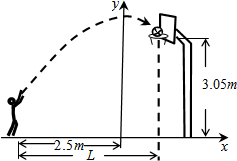 李老师在某次投篮中,球的运动路线是抛物线$y=-\frac{1}{5}{x^2}+3.5$的一部分,其相关数据如图所示,若命中篮圈中心,则他与蓝底的距离L为4米;若身高为1.79米的李老师是跳投命中篮圈中心的,且篮球在离李老师的头顶上方0.25米处出手,那么跳投时他跳离地面的高度为0.21米.
李老师在某次投篮中,球的运动路线是抛物线$y=-\frac{1}{5}{x^2}+3.5$的一部分,其相关数据如图所示,若命中篮圈中心,则他与蓝底的距离L为4米;若身高为1.79米的李老师是跳投命中篮圈中心的,且篮球在离李老师的头顶上方0.25米处出手,那么跳投时他跳离地面的高度为0.21米. 如图,在△ABC中DE∥C,交AB,AC于点D,E,试证明$\frac{AD}{AB}=\frac{DO}{CO}$.
如图,在△ABC中DE∥C,交AB,AC于点D,E,试证明$\frac{AD}{AB}=\frac{DO}{CO}$.