题目内容
18.△ABC∽△A′B′C′,AD、A′D′分别是△ABC和△A′B′C′的角平分线,且比为5:3,下列结论正确的有①②③④.①$\frac{BC}{{{B^'}{C^'}}}=\frac{5}{3}$;②${C_△}_{ABC}:{C_△}_{{A^'}{B^'}{C^'}}=5:3$;③它们的相似比是5:3,;④△ABC和△A′B′C′的高分别为BE、B′E′,则BE:B′E′=5:3.
分析 运用相似三角形的性质:相似三角形的对应边的比、周长的比、对应高、对应中线、对应角平分线的比都等于相似比,相似三角形的面积比等于相似比的平方进行判断即可.
解答 解:∵△ABC∽△A′B′C′,AD、A′D′分别是△ABC和△A′B′C′的角平分线,且比为5:3,
∴对应边的比$\frac{BC}{{{B^'}{C^'}}}=\frac{5}{3}$;对应周长的比${C_△}_{ABC}:{C_△}_{{A^'}{B^'}{C^'}}=5:3$;它们的相似比是5:3,;
△ABC和△A′B′C′的高分别为BE、B′E′,则BE:B′E′=5:3.
故答案为:①②③④.
点评 本题主要考查了相似三角形的性质,相似三角形的对应边的比、周长的比、对应高、对应中线、对应角平分线的比都等于相似比,相似三角形的面积比等于相似比的平方.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
10.已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第2013个图形中直角三角形的个数有( )


| A. | 8048个 | B. | 4024个 | C. | 4026个 | D. | 4028个 |
7.下列从左到右的变形,是分解因式的是( )
| A. | (a+3)(a-3)=a2-9 | B. | x2+x-5=(x-2)(x+3)+1 | C. | a2b+ab2=ab(a+b) | D. | x2+1=x(x+$\frac{1}{x}$) |
8.如果将抛物线y=x2向右平移1个单位,再向上平移2个单位,那么所得的抛物线的表达式是( )
| A. | y=(x-1)2+2 | B. | y=(x-1)2-2 | C. | y=(x+1)2-2 | D. | y=(x+1)2+2 |
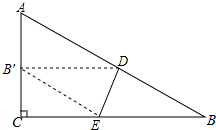 如图是一张直角三角形纸片,∠C=90°,点D在边AB上,若将三角形纸片沿直线DE折叠,使点B落在AC边上,记作点B′,连接B′E.
如图是一张直角三角形纸片,∠C=90°,点D在边AB上,若将三角形纸片沿直线DE折叠,使点B落在AC边上,记作点B′,连接B′E.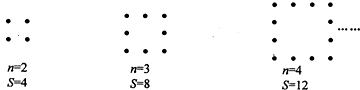
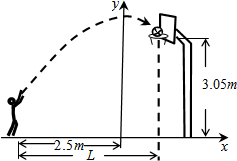 李老师在某次投篮中,球的运动路线是抛物线$y=-\frac{1}{5}{x^2}+3.5$的一部分,其相关数据如图所示,若命中篮圈中心,则他与蓝底的距离L为4米;若身高为1.79米的李老师是跳投命中篮圈中心的,且篮球在离李老师的头顶上方0.25米处出手,那么跳投时他跳离地面的高度为0.21米.
李老师在某次投篮中,球的运动路线是抛物线$y=-\frac{1}{5}{x^2}+3.5$的一部分,其相关数据如图所示,若命中篮圈中心,则他与蓝底的距离L为4米;若身高为1.79米的李老师是跳投命中篮圈中心的,且篮球在离李老师的头顶上方0.25米处出手,那么跳投时他跳离地面的高度为0.21米.