题目内容
2．已知y＞$\sqrt{2x-1}+\sqrt{1-2x}$+2，求$\frac{\sqrt{{y}^{2}-4y+4}}{2-y}$+3-2x的值．分析 根据二次根是有意义的条件可得出x的值，进一步得到y的取值范围，再代入计算即可求解．
解答 解：∵y＞$\sqrt{2x-1}+\sqrt{1-2x}$+2，
∴2x-1=0，
∴x=$\frac{1}{2}$，
∴y＞2，
∴$\frac{\sqrt{{y}^{2}-4y+4}}{2-y}$+3-2x
=$\frac{y-2}{2-y}$+3-1
=-1+3-1
=1．
点评 本题考查了二次根是有意义的条件，掌握二次根是有意义的条件：被开方数大于等于0解题的关键．
练习册系列答案
相关题目
9．
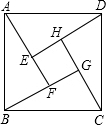如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”，图中的四个直角三角形是全等的，如果大正方形ABCD的面积是小正方形EFGH面积的13倍，那么tan∠ADE的值为（ ）
如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”，图中的四个直角三角形是全等的，如果大正方形ABCD的面积是小正方形EFGH面积的13倍，那么tan∠ADE的值为（ ）| A． | $\frac{3}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{{2\sqrt{13}}}{13}$ |
如图，△ABC中，AB=AC，以AC为直径的⊙O与边AB、BC分别交于点D、E．过E的直线与⊙O相切，与AC的延长线交于点G，与AB交于点F．
几个棱长为1的正方体组成的几何体的三视图如图所示，则这个几何体的体积是5．
11．
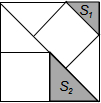有3个正方形按如图所示放置，其中大正方形的边长是1，阴影部分的面积依次记为S1，S2，则S1+S2等于（ ）
有3个正方形按如图所示放置，其中大正方形的边长是1，阴影部分的面积依次记为S1，S2，则S1+S2等于（ ）| A． | $\frac{13}{72}$ | B． | $\frac{13}{36}$ | C． | $\frac{17}{72}$ | D． | $\frac{3}{16}$ |