题目内容
如图6423，在△ABC中，∠C＝90°，BC＝5米，AC＝12米．点M在线段CA上，从C向A运动，速度为1米/秒；同时点N在线段AB上，从A向B运动，速度为2米/秒，运动时间为t秒．
(1)当t为何值时，∠AMN＝∠ANM；
(2)当t为何值时，△AMN的面积最大？并求出这个最大值．
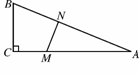
解：(1)由题意，得AM＝12－t，AN＝2t.
∵∠AMN＝∠ANM，
∴AM＝AN，从而12－t＝2t，
解得t＝4秒．
∴当t为4秒时，∠AMN＝∠ANM.
(2)如图56，过点N作NH⊥AC于点H，
∴∠NHA＝∠C＝90°.
∵∠A是公共角，∴△NHA∽△BCA.
∴
＝
，即
＝
，∴NH＝
.
从而有S△AMN＝
(12－t)·＝－
t2＋
t，
∴当t＝6时，S有最大值为
.
图56 图57
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
，
，则
．