题目内容
已知:O为直线AB上的一点,OC⊥OE于点O,射线OF平分∠AOE.
(1)如图4123(1),判断∠COF和∠BOE之间的数量关系?并说明理由;
(2)若将∠COE绕点O旋转至图4123(2)的位置,试问(1)中∠COF和∠BOE之间的数量关系是否发生变化?若不发生变化,请你加以证明,若发生变化,请你说明理由;
(3)若将∠COE绕点O旋转至图4123(3)的位置,继续探究∠COF和∠BOE之间的数量关系,并加以证明.
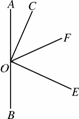
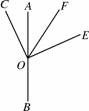
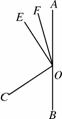
(1) (2) (3)
图4123
解:(1)∵∠COE=90°,∴∠BOE=90°-∠AOC,∠COF= -∠AOC=
-∠AOC= .
.
∴∠BOE=2∠COF.
(2)不发生变化.证明如下:
∵∠COE=90°,
∴∠COF=90°-∠EOF,∠BOE=180°-2∠EOF.
∴∠BOE=2∠COF.
(3)∠BOE+2∠COF=360°.
理由:∵∠COE=90°,∴∠COF=90°+∠EOF,∠BOE=90°+∠BOC=90°+90°-2∠EOF=180°-2∠EOF.
∴∠BOE+2∠COF=360°.

练习册系列答案
相关题目

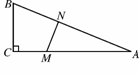


 ∥
∥ 的条件是( ).
的条件是( ). B.
B. ;C.
;C. ; D.
; D.  .
.
