题目内容
17.求21+22+23+…+2n的和,解法如下:解:设S=21+22+23+…+2n①
2S=22+23+…+2n+2n+1②
②-①得S=2n+1-2
所以21+22+23+…+2n=2n+1-2
参照上面的解法,
计算:1+31+32+33+…+3n-1=$\frac{{3}^{n}-1}{2}$.
分析 设S=3°+31+32+33+…+32015+3n-1,然后表示出3S,再相减计算即可得解.
解答 解:设S=3°+31+32+33+…+32015+3n-1,
则3S=31+32+33+…+32015+3n,
∴2S=(31+32+33+…+32015+3n)-(30+31+32+33+…+32015+3n-1)=3n-1
∴S=$\frac{{3}^{n}-1}{2}$,
故答案为:$\frac{{3}^{n}-1}{2}$.
点评 本题主要考查了数字变化规律,利用有理数的乘方的计算,利用整体思想求解是解答此题的关键.

练习册系列答案
相关题目
2.对于数据:80,88,85,85,83,83,84.下列说法中错误的有( )
(1)这组数据的平均数是84; (2)这组数据的众数是85:
(3)这组数据的中位数是84;(4)这组数据的方差是36.
(1)这组数据的平均数是84; (2)这组数据的众数是85:
(3)这组数据的中位数是84;(4)这组数据的方差是36.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
7.下列四个数中最小的数是( )
| A. | 3 | B. | 0 | C. | $-\frac{1}{4}$ | D. | 4 |
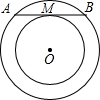 如图,已知两同心圆,大圆的弦AB切小圆于M,若环形的面积为9π,则AB的长是6.
如图,已知两同心圆,大圆的弦AB切小圆于M,若环形的面积为9π,则AB的长是6. △ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB,垂足为D,PE⊥AC,垂足为E.
△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB,垂足为D,PE⊥AC,垂足为E.