题目内容
4.市政府大力扶持大学生创业,小明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价(x)元之间的关系可近似地看做一次函数y=-10x+500.(1)设小明每月获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果小明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于35元,如果小明想要每月获得的利润不低于2000元,那么他每月的成本最多需要多少元?(成本=进价×销售量)
分析 (1)根据利润=每件的利润×销售量,构建二次函数利用配方法确定最大值.
(2)利用(1)中的结果,列出方程即可解决问题.
(3)利用一次函数的增减性,即可解决问题.
解答 (1)解:W=(-10x+500)(x-20)
=-10x2+700x-10000
=-10(x-35)2+2250
∴当x=35时,每月可获得最大利润2250元
(2)-10(x-35)2+2250=2000
得x1=30,x2=40
∴当销售价定为30或40元时,小明每月获得2000元利润.
(3)y=-10x+500
∵-10<0,∴y随x的增大而减小
∴当x取30时,成本最多
即成本=20×(-10×30+500)
=20×200
=4000(元)
点评 本题考查二次函数、一次函数的性质,一元二次方程的应用,解题的关键是搞清楚利润、销售量、进价、销售价之间的关系,学会构建二次函数解决最值问题,属于中考常考题型.

练习册系列答案
相关题目
16.两个数的商为正数,则两个数( )
| A. | 都为正 | B. | 都为负 | C. | 同号 | D. | 异号 |
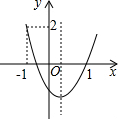 如图,二次函数y=ax2+bx+c的图象,图象经过点(-1,2)和(1,0),给出四个结论:
如图,二次函数y=ax2+bx+c的图象,图象经过点(-1,2)和(1,0),给出四个结论: 如图,一架梯子长25米,斜靠在一面墙上,梯子顶端离地面15米,要使梯子顶端离地24米,则梯子的底部在水平方向上应滑动多少米?
如图,一架梯子长25米,斜靠在一面墙上,梯子顶端离地面15米,要使梯子顶端离地24米,则梯子的底部在水平方向上应滑动多少米?