题目内容
20. 如图,直角ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置,AB的中点D旋转到D′,已知AC=12,BC=5,则线段DD′长为$\frac{13\sqrt{2}}{2}$.
如图,直角ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置,AB的中点D旋转到D′,已知AC=12,BC=5,则线段DD′长为$\frac{13\sqrt{2}}{2}$.
分析 如图,连接CD、CD′.首先证明△DCD′是等腰直角三角形,根据直角三角形斜边中线定理可知,CD=CD′=$\frac{13}{2}$,DD′=$\sqrt{2}$CD即可解决问题.
解答 解:如图,连接CD、CD′.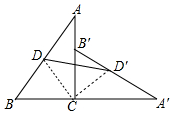
在Rt△ABC中,∵AC=12,BC=5,
∴AB=A′B′=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
∵△ACB,△A′CB′都是直角三角形,BD=DA,A′D′=B′D′,
∴CD=$\frac{1}{2}$AB=$\frac{13}{2}$,CD′=$\frac{1}{2}$A′B′=$\frac{13}{2}$,
∵∠DCD′=∠BCB′=90°(旋转角相等),
∴△DCD′是等腰直角三角形,
∴DD′=$\sqrt{2}$CD=$\frac{13\sqrt{2}}{2}$,
故答案为$\frac{13\sqrt{2}}{2}$.
点评 本题考查旋转的性质、直角三角形斜边中线定理、等腰直角三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,注意旋转角相等的应用,属于中考常考题型.

练习册系列答案
相关题目
11.若等腰三角形的周长为10,一边长为3,则这个等腰三角形的腰长为( )
| A. | 3.5 | B. | 3 | C. | 3.5或3 | D. | 6 |
9.下列方程是一元一次方程的是( )
| A. | 2x=-5 | B. | $\frac{2}{3}$x2=6 | C. | 3x-y=4 | D. | $\frac{4}{y}$+6=8 |
 设直线l1:y=-x+n的图象与y轴交于A点,直线l2:y=-3x-m的图象与y轴交于B点,l1与l2的图象相交于点C(-3,1).
设直线l1:y=-x+n的图象与y轴交于A点,直线l2:y=-3x-m的图象与y轴交于B点,l1与l2的图象相交于点C(-3,1).
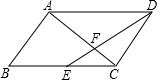 已知平行四边形ABCD中,点E是边BC的中点,DE与AC相交于点F,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{FD}$=$\frac{1}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$ (用$\overrightarrow{a}$,$\overrightarrow{b}$的式子表示)
已知平行四边形ABCD中,点E是边BC的中点,DE与AC相交于点F,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{FD}$=$\frac{1}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$ (用$\overrightarrow{a}$,$\overrightarrow{b}$的式子表示)