题目内容
11．若等腰三角形的周长为10，一边长为3，则这个等腰三角形的腰长为（ ）| A． | 3.5 | B． | 3 | C． | 3.5或3 | D． | 6 |
分析 根据已知的等腰三角形的周长和一边的长，先分清三角形的底和腰，再计算腰长．
解答 解：当3为腰，底边的长为10-3-3=4时，3+3＞4，能构成等腰三角形，所以腰长可以是3；
当3为底，腰的长为（10-3）÷2=3.5时，3.5，3.5，3能构成等腰三角形，所以腰长可以是3.5．
故选：C．
点评 本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．
练习册系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
19．
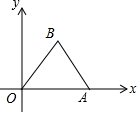如图在平面直角坐标系中，等边三角形OAB的顶点A在x轴上，顶点B在第一象限，若OA=2，则点B关于原点的对称点坐标为（ ）
如图在平面直角坐标系中，等边三角形OAB的顶点A在x轴上，顶点B在第一象限，若OA=2，则点B关于原点的对称点坐标为（ ）| A． | （1，$\sqrt{3}$） | B． | （$\sqrt{3}$，1） | C． | （-1，-$\sqrt{3}$） | D． | （-$\sqrt{3}$，-1） |
如图，有一个英语单词，四个字母都关于直线l对称，请写出这个单词BOOK．
如图，直角ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置，AB的中点D旋转到D′，已知AC=12，BC=5，则线段DD′长为$\frac{13\sqrt{2}}{2}$．
如图：△ABC中，∠A=50°，BE平分∠ABC，CE是△ABC的外角∠ACD的角平分线，则∠E=25°．