题目内容
12.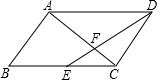 已知平行四边形ABCD中,点E是边BC的中点,DE与AC相交于点F,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{FD}$=$\frac{1}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$ (用$\overrightarrow{a}$,$\overrightarrow{b}$的式子表示)
已知平行四边形ABCD中,点E是边BC的中点,DE与AC相交于点F,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{FD}$=$\frac{1}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$ (用$\overrightarrow{a}$,$\overrightarrow{b}$的式子表示)
分析 根据平行四边形的性质及中点的定义得BC∥AD、BC=AD=2EC,再证△ADF∽△CEF得$\frac{AF}{AC}$=$\frac{2}{3}$,根据$\overrightarrow{FD}$=$\overrightarrow{AD}-\overrightarrow{AF}$=$\overrightarrow{AD}$-$\frac{2}{3}$$\overrightarrow{AC}$=$\overrightarrow{AD}$-$\frac{2}{3}$($\overrightarrow{AB}+\overrightarrow{AD}$)可得答案.
解答 解:∵四边形ABCD是平行四边形,点E是边BC的中点,
∴BC∥AD,BC=AD=2EC,
∴△ADF∽△CEF,$\overrightarrow{BC}=\overrightarrow{AD}=\overrightarrow{b}$,
∴$\frac{AF}{CF}$=$\frac{AD}{EC}$=2,
则$\frac{AF}{AC}$=$\frac{2}{3}$,
∴$\overrightarrow{FD}$=$\overrightarrow{AD}-\overrightarrow{AF}$
=$\overrightarrow{AD}$-$\frac{2}{3}$$\overrightarrow{AC}$
=$\overrightarrow{AD}$-$\frac{2}{3}$($\overrightarrow{AB}+\overrightarrow{AD}$)
=$\overrightarrow{b}$-$\frac{2}{3}$($\overrightarrow{a}$+$\overrightarrow{b}$)
=$\frac{1}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$,
故答案为:$\frac{1}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$.
点评 本题主要考查平行四边形的性质、相似三角形的判定与性质及向量的基本运算,熟练掌握向量的运算法则是解题的关键.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案| A. |  | B. |  | C. |  | D. |  |
 如图,直角ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置,AB的中点D旋转到D′,已知AC=12,BC=5,则线段DD′长为$\frac{13\sqrt{2}}{2}$.
如图,直角ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置,AB的中点D旋转到D′,已知AC=12,BC=5,则线段DD′长为$\frac{13\sqrt{2}}{2}$. 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D. 如图:△ABC中,∠A=50°,BE平分∠ABC,CE是△ABC的外角∠ACD的角平分线,则∠E=25°.
如图:△ABC中,∠A=50°,BE平分∠ABC,CE是△ABC的外角∠ACD的角平分线,则∠E=25°.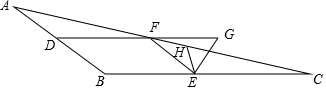 如图,已知:点D、E、F是△ABC的边AB、BC、AC上的点,DF∥BC,EF∥AB,EG平分∠FEC交DF的延长线于点G,EH平分∠BEG交AC于点H,∠EHC=40°,且∠DFE-∠C=130°,则∠B的度数为144°.
如图,已知:点D、E、F是△ABC的边AB、BC、AC上的点,DF∥BC,EF∥AB,EG平分∠FEC交DF的延长线于点G,EH平分∠BEG交AC于点H,∠EHC=40°,且∠DFE-∠C=130°,则∠B的度数为144°.