题目内容
 如图,在平面直角坐标系xOy中,一次函数y=kx+b与反比例函数y=
如图,在平面直角坐标系xOy中,一次函数y=kx+b与反比例函数y=| m |
| x |
| 3 |
| 4 |
(1)求反比例函数和一次函数的解析式;
(2)连接OA,求△AOD的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)作AE⊥x轴于点E,根据tan∠ABO=
,AB=10求出AE、BE,得出A的坐标,代入反比例函数解析式即可求出解析式,再求出B的坐标,把A、B的坐标代入一次函数的解析式,即可求出一次函数的解析式;
(2)求出OD长,根据三角形的面积公式求出即可.
| 3 |
| 4 |
(2)求出OD长,根据三角形的面积公式求出即可.
解答:解:(1)作AE⊥x轴于点E,
∵tan∠ABO=
,AB=10,
∴AE=6,BE=8,
又∵S△ABC=12,
∴
•AC•6=12,
∴AC=4,
∴A(-4,6),
代入反比例函数的解析式求出k=-24,
∴反比例函数的解析式为:y=-
,
 ∵OB=BE-OE=8-4=4,
∵OB=BE-OE=8-4=4,
∴B(4,0),
将A(-4,6)、B(4,0)代入y=kx+b中,得:
,
∴
,
∴一次函数的解析式为:y=-
x+3;
(2)在y=-
x+3中,令x=0,得:y=3,
∴OD=3,
∴S△AOD=
•OD•AC=
×3×4=6.

∵tan∠ABO=
| 3 |
| 4 |
∴AE=6,BE=8,
又∵S△ABC=12,
∴
| 1 |
| 2 |
∴AC=4,
∴A(-4,6),
代入反比例函数的解析式求出k=-24,
∴反比例函数的解析式为:y=-
| 24 |
| x |
 ∵OB=BE-OE=8-4=4,
∵OB=BE-OE=8-4=4,∴B(4,0),
将A(-4,6)、B(4,0)代入y=kx+b中,得:
|
∴
|
∴一次函数的解析式为:y=-
| 3 |
| 4 |
(2)在y=-
| 3 |
| 4 |
∴OD=3,
∴S△AOD=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了一次函数与反比例函数的交点问题,用待定系数法求一次函数、反比例函数的解析式,三角形的面积,解直角三角形等知识点的应用.

练习册系列答案
相关题目
若(x+y-2)2+|4x+3y-7|=0,则x+y的值为( )
| A、0 | B、1 | C、2 | D、3 |
下列各图案,其中是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
下列运算中正确的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 如图,如果从半径为9cm的圆形纸片剪去
如图,如果从半径为9cm的圆形纸片剪去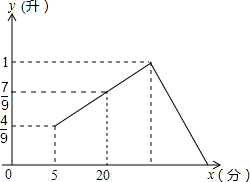 有一个附有进、出水管的水池,每单位时间的进、出水量一定.设从某一时刻开始只进水,5分钟后水池的蓄水量恰好占全池的
有一个附有进、出水管的水池,每单位时间的进、出水量一定.设从某一时刻开始只进水,5分钟后水池的蓄水量恰好占全池的