Question

6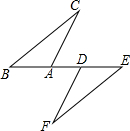．如图，点B、A、D、E在同一直线上，BD=AE，BC∥EF，要使△ABC≌△DEF，则只需添加一个适当的条件是BC=EF或∠BAC=∠EDF．（只填一个即可）

Answer 1

分析 BC=EF或∠BAC=∠EDF，若BC=EF，根据条件利用SAS即可得证；若∠BAC=∠EDF，根据条件利用ASA即可得证．

解答 解：若添加BC=EF，
∵BC∥EF，
∴∠B=∠E，
∵BD=AE，
∴BD-AD=AE-AD，即BA=ED，
在△ABC和△DEF中，
$\left\{\begin{array}{l}{BC=EF}\\{∠B=∠E}\\{BA=ED}\end{array}\right.$，
∴△ABC≌△DEF（SAS）；
若添加∠BAC=∠EDF，
∵BC∥EF，
∴∠B=∠E，
∵BD=AE，
∴BD-AD=AE-AD，即BA=ED，
在△ABC和△DEF中，
$\left\{\begin{array}{l}{∠B=∠E}\\{BA=ED}\\{∠BAC=∠EDF}\end{array}\right.$，
∴△ABC≌△DEF（ASA），
故答案为：BC=EF或∠BAC=∠EDF

点评 此题考查了全等三角形的判定，熟练掌握全等三角形的判定方法是解本题的关键．