题目内容
16.已知A(-2,y1)、B(0,y2)、C(1,y3)三点都在抛物线y=kx2+2kx+k2+k(k<0)的图象上,则y1、y2、y3的大小关系是y1=y2>y3.分析 先求出抛物线的对称轴为直线x=-1,再根据二次函数的对称性和增减性判断.
解答 解:对称轴为直线x=-$\frac{2k}{2•k}$=-1,
∵A(-2,y1)、B(0,y2),
∴A、B是对称点,
∴y1=y2,
∵k<0,
∴x>-1时,y的值随x的增大而减小,
∴y2>y3,
∴y1=y2>y3.
故答案为:y1=y2>y3..
点评 本题考查了二次函数图象上点的坐标特征,主要利用了抛物线的对称性与增减性,求出对称轴是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
7.顺次连接四边形的各边中点所得到的四边形是菱形,那么原四边形是( )
| A. | 任意四边形 | B. | 平行四边形 | C. | 矩形 | D. | 菱形 |
4.下列计算正确的是( )
| A. | x3+x2=x6 | B. | a3•a2=a6 | C. | 3$\sqrt{2}$-$\sqrt{2}$=3 | D. | $\sqrt{14}$×$\sqrt{7}$=7$\sqrt{2}$ |
11.已知x,y是非零实数,则下列计算正确的是( )
| A. | -x-y=-xy | B. | $\frac{1}{x}$+$\frac{1}{y}$=$\frac{1}{x+y}$ | C. | x2y÷(xy2)=xy-1 | D. | $\sqrt{{x}^{2}}$×$\sqrt{(-y)^{2}}$=-xy |
1.如果鸭绿江水位高1m时水位变化记作+1m,那么水位下降0.5m时水位变化记作( )
| A. | -0.5m | B. | 0.5m | C. | 1.5m | D. | -1.5m |
5. 一个几何体零件如图所示,则它的俯视图是( )
一个几何体零件如图所示,则它的俯视图是( )
 一个几何体零件如图所示,则它的俯视图是( )
一个几何体零件如图所示,则它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
 星期天8:00~8:30,燃气公司给平安加气站的储气罐注入天然气.之后,一位工作人员以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(立方米)与时间x(小时)的函数关系如图所示.
星期天8:00~8:30,燃气公司给平安加气站的储气罐注入天然气.之后,一位工作人员以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(立方米)与时间x(小时)的函数关系如图所示.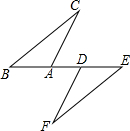 如图,点B、A、D、E在同一直线上,BD=AE,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件是BC=EF或∠BAC=∠EDF.(只填一个即可)
如图,点B、A、D、E在同一直线上,BD=AE,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件是BC=EF或∠BAC=∠EDF.(只填一个即可)