题目内容
1. 如图,在五边形ABCDE中,∠A+∠B+∠E=280°,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是50°.
如图,在五边形ABCDE中,∠A+∠B+∠E=280°,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是50°.
分析 根据五边形的内角和等于540°,由∠A+∠B+∠E=300°,可求∠BCD+∠CDE的度数,再根据角平分线的定义可得∠PDC与∠PCD的角度和,进一步求得∠P的度数.
解答 解:∵五边形的内角和等于540°,∠A+∠B+∠E=280°,
∴∠BCD+∠CDE=540°-280°=260°,
∵∠BCD、∠CDE的平分线在五边形内相交于点O,
∴∠PDC+∠PCD=$\frac{1}{2}$(∠BCD+∠CDE)=130°,
∴∠P=180°-130°=50°.
故答案为:50°.
点评 本题主要考查了多边形的内角和公式,角平分线的定义,熟记公式是解题的关键.注意整体思想的运用.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
6.某校随机抽查了10名参加2017年云南省初中学业水平考试学生的体育成绩,得到的结果如表:
下列说法正确的是( )
| 成绩(分) | 46 | 47 | 48 | 49 | 50 |
| 人数(人) | 1 | 2 | 1 | 2 | 4 |
| A. | 这10名同学的体育成绩的平均数为48 | |
| B. | 这10名同学的体育成绩的中位数为48 | |
| C. | 这10名同学的体育成绩的方差为50 | |
| D. | 这10名同学的体育成绩的众数为50 |
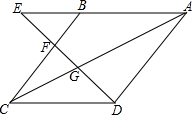 如图,四边形ABCD是菱形,点E在AB延长线上,联结AC,DE,DE分别交BC,AC于点F,G,且CD•AE=AC•AG.
如图,四边形ABCD是菱形,点E在AB延长线上,联结AC,DE,DE分别交BC,AC于点F,G,且CD•AE=AC•AG. 如图,抛物线y=x2-(m+2)x+3(m-1)与x轴的两个交点为A、B,与y轴交于点C,点D为抛物线的顶点,直线y=-2x+m+6经过点B,交y轴于点E(0,6).
如图,抛物线y=x2-(m+2)x+3(m-1)与x轴的两个交点为A、B,与y轴交于点C,点D为抛物线的顶点,直线y=-2x+m+6经过点B,交y轴于点E(0,6).