题目内容
13.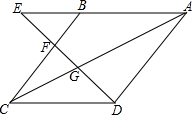 如图,四边形ABCD是菱形,点E在AB延长线上,联结AC,DE,DE分别交BC,AC于点F,G,且CD•AE=AC•AG.
如图,四边形ABCD是菱形,点E在AB延长线上,联结AC,DE,DE分别交BC,AC于点F,G,且CD•AE=AC•AG.求证:(1)△ABC∽△AGE;
(2)AB2=GD•DE.
分析 (1)只要证明$\frac{AB}{AG}$=$\frac{AC}{AE}$,又∠BAC=∠GAE,即可证明△ABC∽△AGE;
(2)只要证明△ADG∽△EDA,可得$\frac{AD}{DE}$=$\frac{DG}{AD}$,推出AD2=DE•DG即可证明;
解答 证明:(1)∵CD•AE=AC•AG.
∴$\frac{CD}{AG}$=$\frac{AC}{AE}$,
∵四边形ABCD是菱形,
∴AB=CD,
∴$\frac{AB}{AG}$=$\frac{AC}{AE}$,∵∠BAC=∠GAE,
∴△ABC∽△AGE,
(2)∵△ABC∽△AGE,
∴∠ACB=∠E,
∵四边形ABCD是菱形,
∴AB=AD,BC∥AD,
∴∠ACB=∠CAD=∠E,
∵∠ADG=∠ADE,
∴△ADG∽△EDA,
∴$\frac{AD}{DE}$=$\frac{DG}{AD}$,
∴AD2=DE•DG,
∴AB2=DE•DG.
点评 本题考查相似三角形的性质、菱形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
18. 如图,一次函数y=kx+b图象经过(1,0),(0,2),则不等式kx+b>0的解为( )
如图,一次函数y=kx+b图象经过(1,0),(0,2),则不等式kx+b>0的解为( )
 如图,一次函数y=kx+b图象经过(1,0),(0,2),则不等式kx+b>0的解为( )
如图,一次函数y=kx+b图象经过(1,0),(0,2),则不等式kx+b>0的解为( )| A. | x>1 | B. | x<1 | C. | x>2 | D. | x<2 |
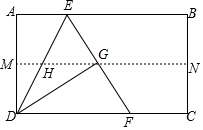 如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为MN,展平后再过点B折叠矩形纸片,使点A落在MN上的点G处,折痕BE与MN相交于点H;再次展平,连接BG,EG,延长EG交BC于点F.有如下结论:
如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为MN,展平后再过点B折叠矩形纸片,使点A落在MN上的点G处,折痕BE与MN相交于点H;再次展平,连接BG,EG,延长EG交BC于点F.有如下结论: 如图,在五边形ABCDE中,∠A+∠B+∠E=280°,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是50°.
如图,在五边形ABCDE中,∠A+∠B+∠E=280°,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是50°.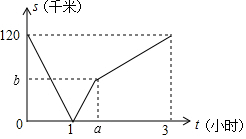 甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论: