题目内容
1. 如图,已知在扇形AOB中,OA=10,∠AOB=36°.将扇形AOB绕点A顺时针旋转,形成新的扇形AO′B′,当O′A经过点B时停止旋转,则点O的运动路径长为4πcm.(结果保留π)
如图,已知在扇形AOB中,OA=10,∠AOB=36°.将扇形AOB绕点A顺时针旋转,形成新的扇形AO′B′,当O′A经过点B时停止旋转,则点O的运动路径长为4πcm.(结果保留π)
分析 根据弧长公式,此题主要是得到∠OBO′的度数,根据等腰三角形的性质即可求解.
解答 解:根据题意,知OA=OB.
又∵∠AOB=36°,
∴∠OBA=72°.
∴点O旋转至O′点所经过的轨迹长度=$\frac{72π×10}{180}$=4πcm.
故答案是:4π.
点评 本题考查了弧长的计算、旋转的性质.解答该题的关键是弄清楚点O的运动轨迹是弧形,然后根据弧长的计算公式求解.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
6. 如图,已知直线AB∥CD,∠C=125°,∠E=80°,那么∠A的大小为( )
如图,已知直线AB∥CD,∠C=125°,∠E=80°,那么∠A的大小为( )
 如图,已知直线AB∥CD,∠C=125°,∠E=80°,那么∠A的大小为( )
如图,已知直线AB∥CD,∠C=125°,∠E=80°,那么∠A的大小为( )| A. | 40° | B. | 45° | C. | 50° | D. | 80° |
13.在一个不透明的袋子中有1个红球和1个白球,这些球除颜色外都相同,现从中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,则两次摸到不同颜色的球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | 1 |
11.今年第一季度,我省固定资产投资完成475.6亿元,这个数据用科学记数法可表示为( )
| A. | 47.56×109元 | B. | 0.4756×1011元 | C. | 4.756×1010元 | D. | 4.756×109元 |
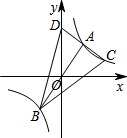 如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{k}{x}$相交于A、B两点,且A点横坐标为2,C是第一象限内双曲线上一点,连接CA并延长交y轴于点D,连接BD,BC.
如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{k}{x}$相交于A、B两点,且A点横坐标为2,C是第一象限内双曲线上一点,连接CA并延长交y轴于点D,连接BD,BC.
 如图,直线a∥b,∠1=120°,∠2=40°,则∠3等于80°.
如图,直线a∥b,∠1=120°,∠2=40°,则∠3等于80°.