题目内容
12.不等式组$\left\{\begin{array}{l}{x+6≥3x+4}\\{5x+5>4x-2}\end{array}\right.$的解集是-7<x≤1.分析 分别解出不等式组中两个不等式的解,合在一起即可得出不等式组的解集.
解答 解:$\left\{\begin{array}{l}{x+6≥3x+4①}\\{5x+5>4x-2②}\end{array}\right.$.
解不等式①,得x≤1;
解不等式②,得x>-7.
∴不等式组的解集为-7<x≤1.
故答案为:-7<x≤1.
点评 本题考查了解一元一次不等式组,解题的关键是熟练掌握解不等式组的方法.本题属于基础题,难度不大,解集该题型题目时,熟练掌握解不等式(或不等式组)的方法是关键.

练习册系列答案
相关题目
3.下列图形中,一定是轴对称图形的是( )
| A. | 等腰三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 直角三角形 |
17.关于x的不等式组$\left\{\begin{array}{l}{x-m>0}\\{2x-3≥3(x-2)}\end{array}\right.$恰有四个整数解,那么m的取值范围为( )
| A. | m≥-1 | B. | m<0 | C. | -1≤m<0 | D. | -1<m<0 |
2.点A的坐标为(2,3),则点A关于原点的对称点A′的坐标为( )
| A. | (-2,3) | B. | (2,-3) | C. | (3,2) | D. | (-2,-3) |
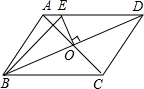 如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OE⊥BD,交AD于点E,如果△ABE的周长为4,那么平行四边形ABCD的周长是8.
如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OE⊥BD,交AD于点E,如果△ABE的周长为4,那么平行四边形ABCD的周长是8.