题目内容
17.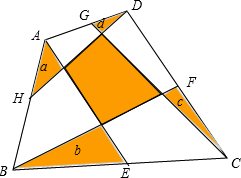 在四边形ABCD中,E、F、G、H分别是四边的中点,分别连接AE、BF、CG、DH,已知图中四个角上的阴影小三角面积分别为a、b、c、d,求中间阴影四边形的面积.
在四边形ABCD中,E、F、G、H分别是四边的中点,分别连接AE、BF、CG、DH,已知图中四个角上的阴影小三角面积分别为a、b、c、d,求中间阴影四边形的面积.
分析 连接BD,由点H、F分别为AB、CD的中点,可得a+d+S1+b+c+S3与S四边形ABCD的关系,S2+S4+S中与S四边形ABCD的关系,同理连接AC可得,a+d+b+c+S2+S4与S四边形ABCD的关系S1+S3+S中与S四边形ABCD的关系,由四式相加,即可求出中间阴影四边形的面积.
解答 解:如图1,连接BD,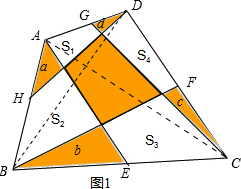
∵点H、F分别为AB、CD的中点,
∴a+d+S1=S△BDH=$\frac{1}{2}$S△ABD,
b+c+S3=S△BDF=$\frac{1}{2}$S△BCD,
∴a+d+S1+b+c+S3=$\frac{1}{2}$(S△ABD+S△BCD)=$\frac{1}{2}$S四边形ABCD①
S△BDH+S△BDF=$\frac{1}{2}$S四边形ABCD,即S四边形BFDH=$\frac{1}{2}$S四边形ABCD,
∴S2+S4+S中=$\frac{1}{2}$S四边形ABCD,②
连接AC,同理可得
∴a+d+b+c+S2+S4=$\frac{1}{2}$S四边形ABCD③,
S1+S3+S中=$\frac{1}{2}$S四边形ABCD④,
①+③=②+④,即:2(a+d+b+c)+S1+S3+S2+S4=S1+S3+S2+S4+2S中,
∴S中=a+b+c+d.
点评 本题主要考查了面积及等积变换,解题的关键是正确的作出辅助线,构造等积三角形.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
5.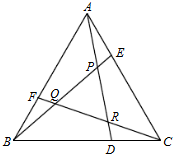 如图所示,已知△ABC面积为l,点D、E、F分别在BC、CA、AB上,且BD=2DC,CE=2EA,AF=2FB,AD、BE、CF两两相交于P、Q、R,则△PQR的面积为( )
如图所示,已知△ABC面积为l,点D、E、F分别在BC、CA、AB上,且BD=2DC,CE=2EA,AF=2FB,AD、BE、CF两两相交于P、Q、R,则△PQR的面积为( )
 如图所示,已知△ABC面积为l,点D、E、F分别在BC、CA、AB上,且BD=2DC,CE=2EA,AF=2FB,AD、BE、CF两两相交于P、Q、R,则△PQR的面积为( )
如图所示,已知△ABC面积为l,点D、E、F分别在BC、CA、AB上,且BD=2DC,CE=2EA,AF=2FB,AD、BE、CF两两相交于P、Q、R,则△PQR的面积为( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{7}$ | D. | $\frac{1}{14}$ |
12.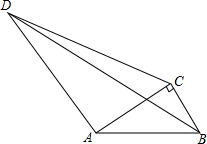 如图,Rt△ABC中,AC=2$\sqrt{3}$,∠CAB=30°,点D和点B分别在线段AC的异侧,且∠ADC=30°,连BD,则BD的最大值为2$\sqrt{7}$+2$\sqrt{3}$.
如图,Rt△ABC中,AC=2$\sqrt{3}$,∠CAB=30°,点D和点B分别在线段AC的异侧,且∠ADC=30°,连BD,则BD的最大值为2$\sqrt{7}$+2$\sqrt{3}$.
 如图,Rt△ABC中,AC=2$\sqrt{3}$,∠CAB=30°,点D和点B分别在线段AC的异侧,且∠ADC=30°,连BD,则BD的最大值为2$\sqrt{7}$+2$\sqrt{3}$.
如图,Rt△ABC中,AC=2$\sqrt{3}$,∠CAB=30°,点D和点B分别在线段AC的异侧,且∠ADC=30°,连BD,则BD的最大值为2$\sqrt{7}$+2$\sqrt{3}$.
2. 如图所示是一个立体图形的三视图,该物体是( )
如图所示是一个立体图形的三视图,该物体是( )
 如图所示是一个立体图形的三视图,该物体是( )
如图所示是一个立体图形的三视图,该物体是( )| A. |  | B. |  | C. |  | D. |  |
6.方程(x-1)(x+2)=0的解是( )
| A. | x=1 | B. | x=-2 | C. | x1=-1,x2=2 | D. | x1=1,x2=-2 |
7.若2×4n×8n=221,则n的值为( )
| A. | 3 | B. | 6 | C. | 5 | D. | 4 |