题目内容
9.从-2,-1,1,2,4这五个数中随机抽取一个数记为a,a的值既能使关于x的方程$\frac{x}{x-2}$-a=$\frac{a}{x-2}$无解,又能使关于x的反比例函数y=$\frac{a}{x}$的图象不经过第二象限的概率是$\frac{2}{5}$.分析 首先确定能使得分式方程无解的a的值,然后确定能使得反比例函数的图象不经过第二象限的a的值,从而利用概率公式求解.
解答 解:方程$\frac{x}{x-2}$-a=$\frac{a}{x-2}$去分母得:
x-a(x-2)=a,
∵关于x的方程$\frac{x}{x-2}$-a=$\frac{a}{x-2}$无解,
∴x=2,
解得:a=2,
由x-a(x-2)=a变形得,
x=$\frac{-a}{1-a}$,
∴当a=1时,方程无解,
∵关于x的反比例函数y=$\frac{a}{x}$的图象不经过第二象限,
∴a>0,
∴a的值为2或1,
∴a的值既能使关于x的方程$\frac{x}{x-2}$-a=$\frac{a}{x-2}$无解,又能使关于x的反比例函数y=$\frac{a}{x}$的图象不经过第二象限的概率是$\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.在x-y=2中,若1<x<2,则y的取值范围是( )
| A. | -2<y<-1 | B. | -1<y<0 | C. | 0<y<1 | D. | 1<y<2 |
15.下列二次根式是最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{1.5}$ | C. | $\sqrt{5}$ | D. | $\sqrt{\frac{1}{2}}$ |
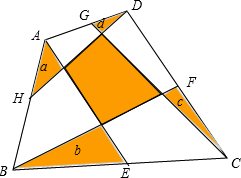 在四边形ABCD中,E、F、G、H分别是四边的中点,分别连接AE、BF、CG、DH,已知图中四个角上的阴影小三角面积分别为a、b、c、d,求中间阴影四边形的面积.
在四边形ABCD中,E、F、G、H分别是四边的中点,分别连接AE、BF、CG、DH,已知图中四个角上的阴影小三角面积分别为a、b、c、d,求中间阴影四边形的面积. 如图,正方形的边长为4,则图中阴影部分的面积为16-4π.
如图,正方形的边长为4,则图中阴影部分的面积为16-4π.