题目内容
5.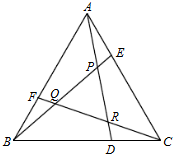 如图所示,已知△ABC面积为l,点D、E、F分别在BC、CA、AB上,且BD=2DC,CE=2EA,AF=2FB,AD、BE、CF两两相交于P、Q、R,则△PQR的面积为( )
如图所示,已知△ABC面积为l,点D、E、F分别在BC、CA、AB上,且BD=2DC,CE=2EA,AF=2FB,AD、BE、CF两两相交于P、Q、R,则△PQR的面积为( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{7}$ | D. | $\frac{1}{14}$ |
分析 连接BR,设△CDR的面积为a,△BRF的面积为b,利用S△CDR+S△BDR+S△BRF=$\frac{1}{3}$,S△BDR+S△BRF+S△ARF=$\frac{2}{3}$,列出方程组求出a的值,同理可求出S△APE=S△BFQ,利用S△PQR=S△BCE-(S△BCF-S△BFQ)-(S△ACD-S△APE-S△CDR)求解即可得出答案.
解答 解:连接BR,设△CDR的面积为a,△BRF的面积为b,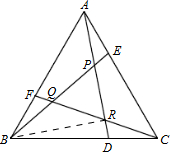
∵BD=2DC,AF=2FB,
∴△BDR的面积为2a,△ARF的面积为2b,
∵已知△ABC面积为l,
∴S△CDR+S△BDR+S△BRF=$\frac{1}{3}$,S△BDR+S△BRF+S△ARF=$\frac{2}{3}$
∴$\left\{\begin{array}{l}{a+2a+b=\frac{1}{3}}\\{2a+b+2b=\frac{2}{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{21}}\\{b=\frac{4}{21}}\end{array}\right.$,
∴△CDR的面积为$\frac{1}{21}$,
同理可得S△APE=S△BFQ=$\frac{1}{21}$,
S△PQR=S△BCE-(S△BCF-S△BFQ)-(S△ACD-S△APE-S△CDR)=$\frac{2}{3}$-$\frac{1}{3}$+S△BFQ-$\frac{1}{3}$+S△APE+S△CDR=S△BFQ+S△APE+S△CDR=$\frac{1}{21}$×3=$\frac{1}{7}$.
故选:C.
点评 本题主要考查了面积与等积变换,解题的关键是正确作出辅助线,求出S△BFQ=S△APE=S△CDR=$\frac{1}{21}$.

 名校课堂系列答案
名校课堂系列答案| A. | $\sqrt{8}$ | B. | $\sqrt{1.5}$ | C. | $\sqrt{5}$ | D. | $\sqrt{\frac{1}{2}}$ |
| A. | 没有最大值,最小值为0 | B. | 没有最大值,没有最小值 | ||
| C. | 最大值为3,最小值为0 | D. | 最大值为3,没有最小值 |
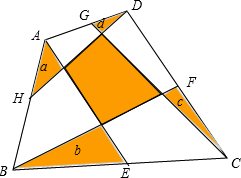 在四边形ABCD中,E、F、G、H分别是四边的中点,分别连接AE、BF、CG、DH,已知图中四个角上的阴影小三角面积分别为a、b、c、d,求中间阴影四边形的面积.
在四边形ABCD中,E、F、G、H分别是四边的中点,分别连接AE、BF、CG、DH,已知图中四个角上的阴影小三角面积分别为a、b、c、d,求中间阴影四边形的面积.