题目内容
1.在一个不透明的袋中装有除颜色外其余都相同的3个小球,其中一个白球、两个红球.如果一次从袋中摸出两个球,那么摸出的两个球都是红球的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
分析 列举出所有情况,看两次都摸到红球的情况数占总情况数的多少即可.
解答 解:摸出的两个球有(白,红1),(白,红2),(红1,红2)3种情况.因此摸出的两个球都是红球的概率=$\frac{1}{3}$,
故选B.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
12.下列不等式是一元一次不等式的是( )
| A. | 5>-2 | B. | x<0 | C. | x+y>0 | D. | x2+x+9≥0 |
6.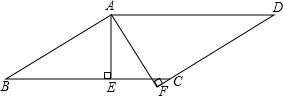 如图,在?ABCD中,AE⊥BC于E,AF⊥DC交DC的延长线于点F,且∠EAF=60°,则∠B等于( )
如图,在?ABCD中,AE⊥BC于E,AF⊥DC交DC的延长线于点F,且∠EAF=60°,则∠B等于( )
 如图,在?ABCD中,AE⊥BC于E,AF⊥DC交DC的延长线于点F,且∠EAF=60°,则∠B等于( )
如图,在?ABCD中,AE⊥BC于E,AF⊥DC交DC的延长线于点F,且∠EAF=60°,则∠B等于( )| A. | 60° | B. | 50° | C. | 70° | D. | 65° |
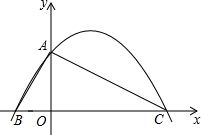 已知,如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.
已知,如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4. 甲骑摩托车从A地去B地,乙开汽车从B地丢A地,同时出发.匀速行驶.各自列达终点后停止.设甲、乙两人间距离为S(单位:千米),甲行驶的时间为t(单位:小时).变量s与t之间的关系如图所示.
甲骑摩托车从A地去B地,乙开汽车从B地丢A地,同时出发.匀速行驶.各自列达终点后停止.设甲、乙两人间距离为S(单位:千米),甲行驶的时间为t(单位:小时).变量s与t之间的关系如图所示.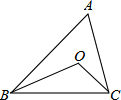 已知:如图:△ABC中,∠B、∠C的角平分线交于点O,若∠A=60°,则∠BOC=120°.
已知:如图:△ABC中,∠B、∠C的角平分线交于点O,若∠A=60°,则∠BOC=120°.