题目内容
11.(1)计算:(π-3)0+$\sqrt{18}$-2sin45°-($\frac{1}{8}$)-1.(2)先化简,再求值:$\frac{a-3}{3{a}^{2}-6a}$÷(a+2-$\frac{5}{a-2}$),其中a满足a2+3a=5.
分析 (1)分别根据0指数幂及负整数指数幂的计算法则、特殊角的三角函数值计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把a2+3a=5代入进行计算即可.
解答 解:(1)原式=1+3$\sqrt{2}$-2×$\frac{\sqrt{2}}{2}$-8
=1+3$\sqrt{2}$-$\sqrt{2}$-8
=2$\sqrt{2}$-7;
(2)原式=$\frac{a-3}{3a(a-2)}$÷$\frac{a-4-5}{a-2}$
=$\frac{a-3}{3a(a-2)}$•$\frac{a-2}{(a+3)(a-3)}$
=$\frac{1}{3{(a}^{2}+3a)}$,
∵a满足a2+3a=5,
∴原式=$\frac{1}{15}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
16.用因式分解法解一元二次方程x(x-3)=x-3时,原方程可化为( )
| A. | (x-1)(x-3)=0 | B. | (x+1)(x-3)=0 | C. | x (x-3)=0 | D. | (x-2)(x-3)=0 |
3.关于中心对称的两个图形,对应线段的关系是( )
| A. | 相等 | B. | 平行 | ||
| C. | 相等且平行 | D. | 相等且平行或相等且在同一直线上 |
1.在一个不透明的袋中装有除颜色外其余都相同的3个小球,其中一个白球、两个红球.如果一次从袋中摸出两个球,那么摸出的两个球都是红球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
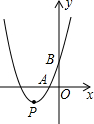 如图,抛物线y=x2+bx+3顶点为P,且分别与x轴、y轴交于A、B两点,点A在点P的右侧,tan∠ABO=$\frac{1}{3}$.
如图,抛物线y=x2+bx+3顶点为P,且分别与x轴、y轴交于A、B两点,点A在点P的右侧,tan∠ABO=$\frac{1}{3}$. 如图,己知∠1=∠2,AC=AD,增加一个条件能使△ABC≌△AEDAB=AE.
如图,己知∠1=∠2,AC=AD,增加一个条件能使△ABC≌△AEDAB=AE.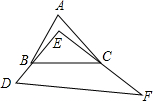 将如图所示的一块直角三角板放置在△ABC上,使三角板的两条直角边DE、EF分别经过点B、C,若∠A=65°,则∠ABE+∠ACE=25°.
将如图所示的一块直角三角板放置在△ABC上,使三角板的两条直角边DE、EF分别经过点B、C,若∠A=65°,则∠ABE+∠ACE=25°.