题目内容
2.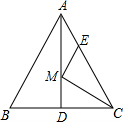 如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=3,EM+CM的最小值为3$\sqrt{3}$.
如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=3,EM+CM的最小值为3$\sqrt{3}$.
分析 要求EM+CM的最小值,需考虑通过作辅助线转化EM,CM的值,从而找出其最小值求解.
解答 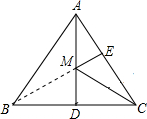 解:连接BE,与AD交于点M.
解:连接BE,与AD交于点M.
∵AD是BC边上的中线,
∴AD⊥BC,
∴AD是BC的垂直平分线,
∴B、C关于AD对称,
∴BE就是EM+CM的最小值.
∵等边△ABC的边长为6,
∴AD=3$\sqrt{3}$,
∵AE=3,
∴CE=AC-AE=6-3=3,
∴BE是AC的垂直平分线,
∴BE=AD=3$\sqrt{3}$,
∵EM+CM=BE
∴EM+CM的最小值为3$\sqrt{3}$.
故答案为3$\sqrt{3}$.
点评 考查等边三角形的性质和轴对称及勾股定理等知识的综合应用,熟练掌握和运用等边三角形的性质以及轴对称的性质是本题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
1.用m个正方形和n个正八边形铺设地面,则m、n满足的条件是( )
| A. | 2m+3n=8 | B. | 3m+2n=8 | C. | m+n=4 | D. | m+2n=6 |
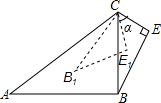 如图,在△ABC和△BCE中,∠CBE=30°,∠BEC=90°,将△BEC绕点C按顺时针方向旋转α(0°<α<180°),在旋转过程中,B的对应点为B1,E的对应点为E1,设直线B1E1与直线BE交于点F,与直线CB交于点Q,当△BPQ为等腰三角形时,α的大小是30°,75°或165°.
如图,在△ABC和△BCE中,∠CBE=30°,∠BEC=90°,将△BEC绕点C按顺时针方向旋转α(0°<α<180°),在旋转过程中,B的对应点为B1,E的对应点为E1,设直线B1E1与直线BE交于点F,与直线CB交于点Q,当△BPQ为等腰三角形时,α的大小是30°,75°或165°.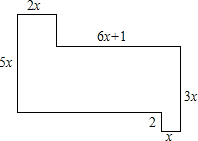 如图的面积为22x2+4x (以x来表示)
如图的面积为22x2+4x (以x来表示) 请只用无刻度的直尺作图:在图中的正方形网格边长均为1,在图(1)中作一个面积为12的菱形;在图(2)中作一个面积为13的正方形.
请只用无刻度的直尺作图:在图中的正方形网格边长均为1,在图(1)中作一个面积为12的菱形;在图(2)中作一个面积为13的正方形.