题目内容
 如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF.
如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF.(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.
考点:相似三角形的判定与性质,等腰直角三角形,三角形中位线定理
专题:几何综合题,压轴题
分析:(1)根据等腰三角形的性质,可得AM是高线、顶角的角平分线,根据直角三角形的性质,可得∠EAB+∠EBA=90°,根据三角形外角的性质,可得答案;
(2)根据三角形中位线的性质,可得MF与AC的关系,根据等量代换,可得MF与BD的关系,根据等腰直角三角形,可得BM与NM的关系,根据等量代换,可得NM与BC的关系,根据同角的余角相等,可得∠CBD与∠NMF的关系,根据两边对应成比例且夹角相等的两个三角形相似,可得答案.
(2)根据三角形中位线的性质,可得MF与AC的关系,根据等量代换,可得MF与BD的关系,根据等腰直角三角形,可得BM与NM的关系,根据等量代换,可得NM与BC的关系,根据同角的余角相等,可得∠CBD与∠NMF的关系,根据两边对应成比例且夹角相等的两个三角形相似,可得答案.
解答:(1)答:△BMN是等腰直角三角形.
证明:∵AB=AC,点M是BC的中点,
∴AM⊥BC,AM平分∠BAC.
∵BN平分∠ABE,
∠EBN=∠ABN.
∵AC⊥BD,
∴∠AEB=90°,
∴∠EAB+∠EBA=90°,
∴∠MNB=∠NAB+∠ABN=
(∠BAE+∠ABE)=45°.
∴△BMN是等腰直角三角形;
(2)答:△MFN∽△BDC.
证明:∵点F,M分别是AB,BC的中点,
∴FM∥AC,FM=
AC.
∵AC=BD,
∴FM=
BD,即
=
.
∵△BMN是等腰直角三角形,
∴NM=BM=
BC,即
=
,
∴
=
.
∵AM⊥BC,
∴∠NMF+∠FMB=90°.
∵FM∥AC,
∴∠ACB=∠FMB.
∵∠CEB=90°,
∴∠ACB+∠CBD=90°.
∴∠CBD+∠FMB=90°,
∴∠NMF=∠CBD.
∴△MFN∽△BDC.
证明:∵AB=AC,点M是BC的中点,
∴AM⊥BC,AM平分∠BAC.
∵BN平分∠ABE,
∠EBN=∠ABN.
∵AC⊥BD,
∴∠AEB=90°,
∴∠EAB+∠EBA=90°,
∴∠MNB=∠NAB+∠ABN=
| 1 |
| 2 |
∴△BMN是等腰直角三角形;
(2)答:△MFN∽△BDC.
证明:∵点F,M分别是AB,BC的中点,
∴FM∥AC,FM=
| 1 |
| 2 |
∵AC=BD,
∴FM=
| 1 |
| 2 |
| FM |
| BD |
| 1 |
| 2 |
∵△BMN是等腰直角三角形,
∴NM=BM=
| 1 |
| 2 |
| NM |
| BC |
| 1 |
| 2 |
∴
| FM |
| BD |
| NM |
| BC |
∵AM⊥BC,
∴∠NMF+∠FMB=90°.
∵FM∥AC,
∴∠ACB=∠FMB.
∵∠CEB=90°,
∴∠ACB+∠CBD=90°.
∴∠CBD+∠FMB=90°,
∴∠NMF=∠CBD.
∴△MFN∽△BDC.
点评:本题考查了相似三角形的判定与性质,利用了锐角是45°的直角三角形是等腰直角三角形,两边对应成比例且夹角相等的两个三角形相似.

练习册系列答案
相关题目
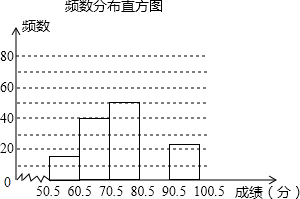 某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分100分)作样本进行统计分析,请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分100分)作样本进行统计分析,请根据尚未完成的频率分布表和频数分布直方图,解答下列问题: 黔东南州某校九年级某班开展数学活动,小明和小军合作用一副三角板测量学校的旗杆,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,已知小明和小军相距(BD)6米,小明的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,参考数据:
黔东南州某校九年级某班开展数学活动,小明和小军合作用一副三角板测量学校的旗杆,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,已知小明和小军相距(BD)6米,小明的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,参考数据: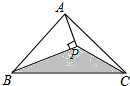 如图,△ABC的面积为4cm2,BP平分∠ABC,且AP⊥BP于P,则△PBC的面积为
如图,△ABC的面积为4cm2,BP平分∠ABC,且AP⊥BP于P,则△PBC的面积为