题目内容
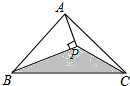 如图,△ABC的面积为4cm2,BP平分∠ABC,且AP⊥BP于P,则△PBC的面积为
如图,△ABC的面积为4cm2,BP平分∠ABC,且AP⊥BP于P,则△PBC的面积为考点:等腰三角形的判定与性质,三角形的面积
专题:
分析:延长AP交BC于D,根据等腰三角形三线合一的性质可得AP=PD,再根据等底等高的三角形的面积相等可得S△ABP=S△DBP,S△ACP=S△DCP,然后求出△PBC的面积的面积等于
S△ABC,再进行计算即可得解.
| 1 |
| 2 |
解答: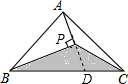 解:如图,延长AP交BC于D,
解:如图,延长AP交BC于D,
∵BP平分∠ABC,AP⊥BP,
∴AP=PD,
∴S△ABP=S△DBP,S△ACP=S△DCP,
∴△PBC的面积=S△DBP+S△DCP=
S△ABC=
×4=2cm2.
故答案为:2.
 解:如图,延长AP交BC于D,
解:如图,延长AP交BC于D,∵BP平分∠ABC,AP⊥BP,
∴AP=PD,
∴S△ABP=S△DBP,S△ACP=S△DCP,
∴△PBC的面积=S△DBP+S△DCP=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:2.
点评:本题考查了等腰三角形的判定与性质,三角形的面积,主要利用了等底等高的三角形的面积相等,作辅助线构造出等腰三角形是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF.
如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF. 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值=
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值=