题目内容
18.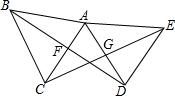 如图,AB=AD,AC=AE,∠BAC=∠DAE,DB交AC于F,且BF=DF,CE交AD于G.求证:CG=EG.
如图,AB=AD,AC=AE,∠BAC=∠DAE,DB交AC于F,且BF=DF,CE交AD于G.求证:CG=EG.
分析 先证明△BAD≌△CAE,得到∠AEC=∠ADB=∠ACE=∠ABD,根据BF=DF,AB=AD,得到AF垂直平分BD,再证明∠AEC+∠EAD=90°,得到∠AGE=90°,即AD⊥CE,根据AC=AE,所以CH=EH.
解答 解:∵AB=AD,BF=DF,AF=AF
∴△BAF≌△DAF
∴∠BAF=∠DAF
∵∠BAC=∠DAE
∴∠BAC=∠CAD=∠DAE
∵AC=AE;AG=AG;∠CAG=∠EAG
∴△AGC≌△AGE
∴CG=EG
点评 本题考查了全等三角形的判定与性质、等腰三角形的性质,解决本题的关键是证明三角形的全等

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
10.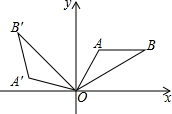 如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )
如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )
 如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )
如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )| A. | (-2,2$\sqrt{2}$) | B. | (-2$\sqrt{2}$,2) | C. | ($\sqrt{2}$,-$\sqrt{2}$) | D. | (-$\sqrt{2}$,$\sqrt{2}$) |
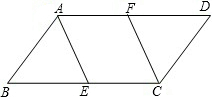 已知:如图,在?ABCD中,E、F分别是BC、AD上的点,BE=DF.
已知:如图,在?ABCD中,E、F分别是BC、AD上的点,BE=DF.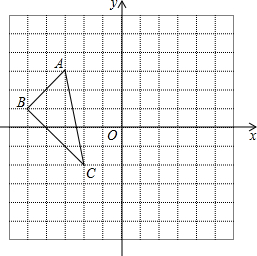 按要求画出图形:
按要求画出图形: 在△ABC中,D是AB的中点,E是AC的中点,BC=12,则DE=6.
在△ABC中,D是AB的中点,E是AC的中点,BC=12,则DE=6.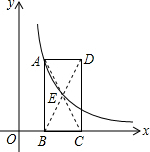 已知如图:矩形ABCD的边BC在x轴上,E为对角线AC、BD的交点,点B、D的坐标分别为B(1,0),D(3,3).
已知如图:矩形ABCD的边BC在x轴上,E为对角线AC、BD的交点,点B、D的坐标分别为B(1,0),D(3,3).
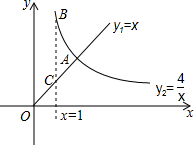 如图,直线和双曲线分别是函数y1=x(x≥0),y2=$\frac{4}{x}$(x>0)的图象,则以下结论:
如图,直线和双曲线分别是函数y1=x(x≥0),y2=$\frac{4}{x}$(x>0)的图象,则以下结论: