题目内容
13.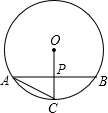 如图,在⊙O中,半径OC⊥弦AB于P,且P为OC的中点,则∠BAC的度数是( )
如图,在⊙O中,半径OC⊥弦AB于P,且P为OC的中点,则∠BAC的度数是( )| A. | 45° | B. | 60° | C. | 25° | D. | 30° |
分析 连接OB,根据OC⊥AB,P为OC的中点可得出OP=$\frac{1}{2}$OB,故∠OBP=30°,由直角三角形的性质得出∠BOP的度数,根据圆周角定理即可得出结论.
解答  解:连接OB,
解:连接OB,
∵OC⊥AB,P为OC的中点,
∴OP=$\frac{1}{2}$OB,
∴∠OBP=30°,
∴∠BOP=90°-30°=60°,
∴∠BAC=$\frac{1}{2}$∠BOP=30°.
故选D.
点评 本题考查的是垂径定理,根据题意作出辅助线,利用直角三角形的性质求解是解答此题的关键.

练习册系列答案
相关题目
8.下列说法错误的是( )
| A. | 棱锥的侧面都是三角形 | B. | 棱柱的侧面不都是长方形 | ||
| C. | 正棱锥的所有侧棱都相等 | D. | 棱柱的所有棱都相等 |
 已知:如图,点B、F、E、C在同一条直线上,AB∥CD,且AB=CD,BF=CE.
已知:如图,点B、F、E、C在同一条直线上,AB∥CD,且AB=CD,BF=CE.