题目内容
15. 如图,AB∥CH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,求GH的长.
如图,AB∥CH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,求GH的长.
分析 根据平行线分线段成比例定理,由AB∥GH,得出$\frac{GH}{AB}=\frac{CH}{BC}$,由GH∥CD,得出$\frac{GH}{CD}=\frac{BH}{BC}$,将两个式子相加,即可求出GH的长.
解答 解:∵AB∥CH∥CD,
∴△CGH∽△ABC,△BGH∽△BCD,
∴$\frac{GH}{AB}=\frac{CH}{BC}$,$\frac{GH}{CD}=\frac{BH}{BC}$,
∴$\frac{GH}{AB}+\frac{GH}{CD}=\frac{GH}{BC}+\frac{BH}{BC}$=1,
∵AB=2,CD=3,
∴$\frac{GH}{2}+\frac{GH}{3}$=1,
∴GH=$\frac{6}{5}$.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.如果把分式$\frac{x+y}{2y}$中的x、y的值都扩大2倍,那么分式的值( )
| A. | 扩大2倍 | B. | 扩大6倍 | C. | 扩大3倍 | D. | 不变 |
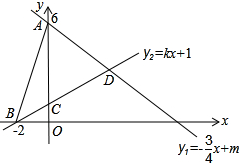 已知如图,直线${l_1}:{y_1}=-\frac{3}{4}x+m$与y轴交于A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.求:
已知如图,直线${l_1}:{y_1}=-\frac{3}{4}x+m$与y轴交于A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.求: