题目内容
已知关于x的方程
=4的解是正数,则m的取值范围为 .
| 2x+m |
| x-2 |
考点:分式方程的解
专题:
分析:先解关于x的分式方程,求得x的值,然后再依据“解是正数”建立不等式求m的取值范围.
解答:解:原方程整理得:2x+m=4x-8,
解得:2x=m+8,
∴x=
(m+8),
∵x>0,
∴m+8>0,
∴m>-8.①
又∵原式是分式方程,
∴x≠2,
∴m+8≠4,
∴m≠-4.②
由①②可得,则m的取值范围为m>-8且m≠-4.
故答案为:m>-8且m≠-4.
解得:2x=m+8,
∴x=
| 1 |
| 2 |
∵x>0,
∴m+8>0,
∴m>-8.①
又∵原式是分式方程,
∴x≠2,
∴m+8≠4,
∴m≠-4.②
由①②可得,则m的取值范围为m>-8且m≠-4.
故答案为:m>-8且m≠-4.
点评:本题考查了分式方程的解,由于我们的目的是求m的取值范围,根据方程的解列出关于m的不等式,另外,解答本题时,易漏掉分母不等于0这个隐含的条件,这应引起足够重视.

练习册系列答案
相关题目
 如图,正方形ABCD的边长为4cm,则它的外接圆的半径长为( )
如图,正方形ABCD的边长为4cm,则它的外接圆的半径长为( )A、
| ||
B、4
| ||
C、3
| ||
D、2
|
某商店把一件商品按进价增加20%作为定价,可是总卖不出去,后来老板把定价降低20%,以48元的价格出售,很快就卖出了,则老板卖出这件商品的盈亏情况是( )
| A、亏2元 | B、亏4元 |
| C、赚4元, | D、不亏不赚 |
下列调查方式合适的是( )
| A、为了了解电视机的使用寿命,采用普查的方式 |
| B、为了了解全国中学生的视力状况,采用普查的方式 |
| C、对载人航天器“神舟六号”零部件的检查,采用抽样调查的方式 |
| D、为了了解人们保护水资源的意识,采用抽样调查的方式 |
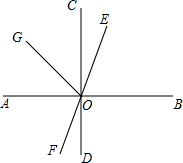 如图,已知直线AB⊥CD于O,EF过点O,OG平分∠AOE,∠FOD=28°,求∠BOE和∠AOG的度数.
如图,已知直线AB⊥CD于O,EF过点O,OG平分∠AOE,∠FOD=28°,求∠BOE和∠AOG的度数.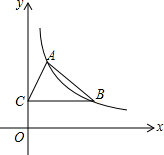 如图,反比例函数y=
如图,反比例函数y=