题目内容
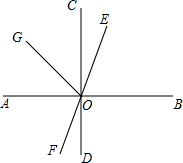 如图,已知直线AB⊥CD于O,EF过点O,OG平分∠AOE,∠FOD=28°,求∠BOE和∠AOG的度数.
如图,已知直线AB⊥CD于O,EF过点O,OG平分∠AOE,∠FOD=28°,求∠BOE和∠AOG的度数.考点:垂线,角平分线的定义
专题:
分析:首先根据垂线的定义可得∠COB=90°,根据对顶角相等可得∠COE的度数,进而可得∠BOE的度数,再根据邻补角的性质可得∠AOE,最后利用角平分线的性质可得∠AOG的度数.
解答:解:∵AB⊥CD,
∴∠COB=90°,
∵∠FOD=28°,
∴∠COE=28°,
∴∠BOE=90°-28°=62°,
∴∠AOE=180°-62°=118°,
∵OG平分∠AOE,
∴∠AOG=
∠AOE=59°.
∴∠COB=90°,
∵∠FOD=28°,
∴∠COE=28°,
∴∠BOE=90°-28°=62°,
∴∠AOE=180°-62°=118°,
∵OG平分∠AOE,
∴∠AOG=
| 1 |
| 2 |
点评:此题主要考查了角平分线,对顶角的性质,以及垂线定义,关键是掌握当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.

练习册系列答案
相关题目
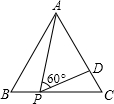 如图,如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长是( )
如图,如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长是( )A、
| ||
B、
| ||
C、
| ||
D、
|
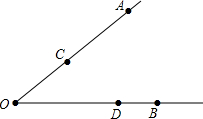 如图,已知点A、点C、点B、点D分别在∠O的边上.
如图,已知点A、点C、点B、点D分别在∠O的边上.(1)请根据下列语句画出图形:
①作直线AB;
②作射线CD与直线AB相交于点F;
③取OD的中点M,连接CM.
(2)若∠CMO=∠CMD=x°,则x=
已知|a|=4,b2=9且|a+b|≠a+b,则代数式a-b的值为( )
| A、1或7 | B、1或-7 |
| C、-1或-7 | D、±1或±7 |
已知二次函数y=ax2+bx+c的图象过点A(1,2),B(3,2),C(5,7).若点M(-2,y1),N(-1,y2),也在该二次函数y=ax2+bx+c的图象上,则下列结论正确的是( )
| A、y1=y2 |
| B、y1<y2 |
| C、y1>y2 |
| D、y1≤y2 |
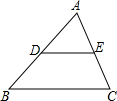 如图,已知DE∥BC,且∠ADE=62°,∠DEC=112°,则∠B=
如图,已知DE∥BC,且∠ADE=62°,∠DEC=112°,则∠B=