题目内容
如图，正方形ABCD的边长为4cm，则它的外接圆的半径长为（ ）A、
| ||
B、4
| ||
C、3
| ||
D、2
|
考点：正多边形和圆
专题：
分析：连接OA，OD，根据圆周角定理可知∠AOD=90°，故△AOD是等腰直角三角形，再根据勾股定理求出OA的长即可．
解答：
解：∵连接OA，OD，
∵四边形ABCD是正方形，
∴∠AOD=90°，
∴△AOD是等腰直角三角形，
∴OA2+OD2=AD2，即2OA2=42，解得OA=2
（cm）．
故选D．
解：∵连接OA，OD，∵四边形ABCD是正方形，
∴∠AOD=90°，
∴△AOD是等腰直角三角形，
∴OA2+OD2=AD2，即2OA2=42，解得OA=2
| 2 |
故选D．
点评：本题考查的是正多边形和圆，熟知正方形的性质是解答此题的关键．
练习册系列答案
相关题目
△ABC中，∠B=67°，∠C=33°，AD是△ABC的角平分线，则∠ADC的度数是（ ）
| A、107° | B、112° |
| C、117° | D、122° |
两个边长为1的正方形，如图所示，让一个正方形的顶点与另一个正方形中心重合，不难知道重合部分的面积为
如图，已知点B在线段CF上，AB∥CD，AD∥BC，则S△AEF与S△BCE的大小关系
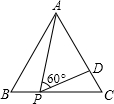如图，如图，等边△ABC的边长为3，P为BC上一点，且BP=1，D为AC上一点，若∠APD=60°，则CD的长是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
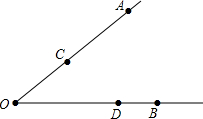如图，已知点A、点C、点B、点D分别在∠O的边上．