题目内容
对于抛物线y=ax2+bx+c,若它的各项系数a,b,c满足b2=a2+c2,则称抛物线为“勾股抛物线”.现有“勾股抛物线y=ax2+bx+c”过点(1,0),则该抛物线的对称轴是 .
考点:二次函数图象上点的坐标特征
专题:新定义
分析:先根据二次函数图象上点的坐标特征得到a+b+c=0,则c=-(a+b),再根据新定义得到b2=a2+c2,接着消去c得到b=-a,然后根据二次函数的性质求抛物线对称轴.
解答:解:∵勾股抛物线y=ax2+bx+c过点(1,0),
∴a+b+c=0,
∴c=-(a+b),
∵b2=a2+c2,
∴b2=a2+(a+b)2,
∴b=-a,
∴抛物线的对称轴为直线x=-
=-
=
.
故答案为直线x=
.
∴a+b+c=0,
∴c=-(a+b),
∵b2=a2+c2,
∴b2=a2+(a+b)2,
∴b=-a,
∴抛物线的对称轴为直线x=-
| b |
| 2a |
| -a |
| 2a |
| 1 |
| 2 |
故答案为直线x=
| 1 |
| 2 |
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
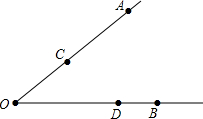 如图,已知点A、点C、点B、点D分别在∠O的边上.
如图,已知点A、点C、点B、点D分别在∠O的边上.(1)请根据下列语句画出图形:
①作直线AB;
②作射线CD与直线AB相交于点F;
③取OD的中点M,连接CM.
(2)若∠CMO=∠CMD=x°,则x=
一个几何体的三视图如图所示.后视图为中心对称的一项是( )
A、 |
B、 |
C、 |
D、 |
已知二次函数y=ax2+bx+c的图象过点A(1,2),B(3,2),C(5,7).若点M(-2,y1),N(-1,y2),也在该二次函数y=ax2+bx+c的图象上,则下列结论正确的是( )
| A、y1=y2 |
| B、y1<y2 |
| C、y1>y2 |
| D、y1≤y2 |
 如图,已知菱形OABC顶点B的坐标为(8,4).顶点A在x轴的正半轴上,反比例函数y=
如图,已知菱形OABC顶点B的坐标为(8,4).顶点A在x轴的正半轴上,反比例函数y=| k |
| x |
| A、32 | B、24 | C、20 | D、12 |
下列所描述的事件是必然事件的是( )
| A、打开电视机,正在转播足球赛 |
| B、射击运动员射击一次,命中10环 |
| C、通常水加热到100℃时沸腾 |
| D、在一个只装有红球袋中摸出白球 |
 铁丝AB=12米,AD=13米,AC=15米,又测得地面上B,C两点之间距离是9米,B,D两点之间距离5米,则电线杆和地面是否垂直,为什么?
铁丝AB=12米,AD=13米,AC=15米,又测得地面上B,C两点之间距离是9米,B,D两点之间距离5米,则电线杆和地面是否垂直,为什么?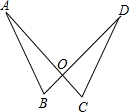 如图,线段AC、DB的交于点O,且AC=BD,OB=OC,小明在探索△ABO与△DCO全等时,他的思考过程如下:因为AC=DB,∠AOB=∠DOC,OB=OC,所以△ABD≌△DCO.
如图,线段AC、DB的交于点O,且AC=BD,OB=OC,小明在探索△ABO与△DCO全等时,他的思考过程如下:因为AC=DB,∠AOB=∠DOC,OB=OC,所以△ABD≌△DCO.